题目内容
如果函数y=2sinx+acosx的值域为[-3,3],则a等于
- A.

- B.±1
- C.±

- D.±

C
分析:把函数解析式提取 ,利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的值域得到函数的值域,比较已知的值域列出关于a的方程,求出方程的解得到a的值.
,利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的值域得到函数的值域,比较已知的值域列出关于a的方程,求出方程的解得到a的值.
解答:y=2sinx+acosx
= sin(x+θ),(sinθ=
sin(x+θ),(sinθ=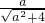 ,cosθ=
,cosθ=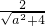 )
)
∵函数的值域为[-3,3],
∴ =3,解得:a=±
=3,解得:a=± .
.
故选C
点评:此题考查了两角和与差的正弦函数公式,以及正弦函数的定义域及值域,利用三角形函数的恒等变形把函数解析式化为一个角的正弦函数是解本题的关键.
分析:把函数解析式提取
 ,利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的值域得到函数的值域,比较已知的值域列出关于a的方程,求出方程的解得到a的值.
,利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的值域得到函数的值域,比较已知的值域列出关于a的方程,求出方程的解得到a的值.解答:y=2sinx+acosx
=
 sin(x+θ),(sinθ=
sin(x+θ),(sinθ=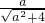 ,cosθ=
,cosθ=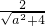 )
)∵函数的值域为[-3,3],
∴
 =3,解得:a=±
=3,解得:a=± .
.故选C
点评:此题考查了两角和与差的正弦函数公式,以及正弦函数的定义域及值域,利用三角形函数的恒等变形把函数解析式化为一个角的正弦函数是解本题的关键.

练习册系列答案
相关题目
 对称,那么|φ|的最小值为
对称,那么|φ|的最小值为



 中心对称,那么|φ|的最小值为 .
中心对称,那么|φ|的最小值为 .