Question

【题目】如图，隔河看两目标A、B，但不能到达，在岸边选取相距 km的C、D两点，并测得∠ACB=75°，∠BCD=45°，∠ADC=30°，∠ADB=45°（A、B、C、D在同一平面内），求两目标A、B之间的距离．

Answer 1

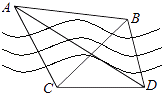
【答案】解：在△ACD中，∠ADC=30°，∠ACD=120°，∴∠CAD=30°． ∴AC=CD= ．
在△BDC中，∠CBD=180°﹣（45°+75°）=60°．
由正弦定理，得BC= ．
由余弦定理，得AB2=AC2+BC2﹣2ACBCcos∠BCA
= =5．
∴AB= ．
∴两目标A、B之间的距离为 km．

【解析】利用△ACD的边角关系得出AC，在△BCD中，由正弦定理即可得出BC，在△ACB中利用余弦定理即可得出AB．