题目内容
P与F分别是抛物线x2=-4y上的点和焦点，已知点A（1，-2），为使|PA|+|PF|取最小值，则P点坐标为
（1，-
）
| 1 |
| 4 |
（1，-
）
．| 1 |
| 4 |
分析：根据抛物线的定义可知，P点到F点的距离等于P点到准线y=1的距离，从而|PA|+|PF|的最小值即为A点到准线的距离，进而可求P点坐标．
解答：解：根据抛物线的定义可知，P点到F点的距离等于P点到准线y=1的距离，
从而|PA|+|PF|的最小值即为A点到准线的距离，
故P在过A点做准线的垂线，和抛物线的交点时|PA|+|PF|取最小值，
此时P点坐标为(1，-
)；
故答案为：(1，-
)．
从而|PA|+|PF|的最小值即为A点到准线的距离，
故P在过A点做准线的垂线，和抛物线的交点时|PA|+|PF|取最小值，
此时P点坐标为(1，-
| 1 |
| 4 |
故答案为：(1，-
| 1 |
| 4 |
点评：本题以抛物线的标准方程为载体，考查抛物线的定义，考查抛物线的简单性质．
练习册系列答案
一线名师口算应用题天天练一本全系列答案
小学学习好帮手系列答案
相关题目
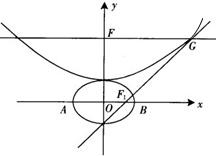设b＞0，椭圆方程为
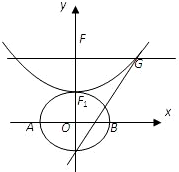设b＞0，椭圆方程为
，0），对应于这个焦点的准线方程为x=-
(本小题满分14分)设b>0，椭圆方程为
，抛物线方程为
.如图4所示,过点F(0,b+2)作x轴的平行线，与抛物线在
.
，0），对应于这个焦点的准线方程为x=-