题目内容
若y=log2(x2-ax-a)在区间(-∞,1-| 3 |
分析:先将原函数分解为两个基本函数,y=log2t,t=x2-ax-a再利用复合函数的单调性求解.
解答:解:令t=x2-ax-a>0
对称轴为x=
y=log2t在(0,+∞)上单调增,y=log2(x2-ax-a)在区间(-∞,1-
)上是减函数
所以t=x2-ax-a在函数的定义域上为减函数(同增异减)
所以(-∞,1-
)?(-∞,
],
所以
≥1-
解得a≥2(1-
) ①
又t在真数位置,故t1-
≥0,即t1-
=4-2
-a(2-
)≥ 0,解得a≤2 ②
由①②得2≥a≥2(1-
);
故答案为2≥a≥2(1-
).
对称轴为x=
| a |
| 2 |
y=log2t在(0,+∞)上单调增,y=log2(x2-ax-a)在区间(-∞,1-
| 3 |
所以t=x2-ax-a在函数的定义域上为减函数(同增异减)
所以(-∞,1-
| 3 |
| a |
| 2 |
所以
| a |
| 2 |
| 3 |
解得a≥2(1-
| 3 |
又t在真数位置,故t1-
| 3 |
| 3 |
| 3 |
| 3 |
由①②得2≥a≥2(1-
| 3 |
故答案为2≥a≥2(1-
| 3 |
点评:本题主要考查复合函数的单调性,要注意两点:一是同增异减,二是定义域.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
若y=-log2(x2-ax-a)在区间(-∞,1-
)上是增函数,则a的取值范围是( )
| 3 |
A、[2-2
| ||
B、[2-2
| ||
C、(2-2
| ||
D、(2-2
|
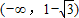 上是减函数,则a的取值范围是 .
上是减函数,则a的取值范围是 .