题目内容
10.已知f(x)=$\left\{\begin{array}{l}{-2(x-\frac{1}{2})^{2}+1\\;x∈[0,\frac{1}{2})}\\{-2x+2\\;x∈[\frac{1}{2},1]}\end{array}\right.$,求函数y=f[f(x)]-x的所有零点之和.分析 利用函数的解析式,化简函数y=f[f(x)]-x的表达式,求出函数的零点,即可求解.
解答 解:f(x)=$\left\{\begin{array}{l}{-2(x-\frac{1}{2})^{2}+1\\;x∈[0,\frac{1}{2})}\\{-2x+2\\;x∈[\frac{1}{2},1]}\end{array}\right.$,
x∈[0,$\frac{1}{2}$)时,f(x)∈[$\frac{1}{2}$,1).x∈[$\frac{1}{2}$,$\frac{3}{4}$)时,f(x)∈($\frac{1}{2}$,1].x∈[$\frac{3}{4}$,1]时,f(x)∈[0,$\frac{1}{2}$].
函数y=f[f(x)]-x=$\left\{\begin{array}{l}-2[-2{(x-\frac{1}{2})}^{2}+1]+2-x&;x∈[0,\frac{1}{2})\\-2(-2x+2)+2-x&;x∈[\frac{1}{2},\frac{3}{4})\\-2{(-2x+2-\frac{1}{2})}^{2}+1-x;x∈[\frac{3}{4},1]&\end{array}\right.$
=$\left\{\begin{array}{l}4{x}^{2}-5x+1&;x∈[0,\frac{1}{2})\\ 3x-2&;x∈[\frac{1}{2},\frac{3}{4})\\-2{(-2x+\frac{3}{2})}^{2}+1-x;x∈[\frac{3}{4},1]&\end{array}\right.$,
函数y=f[f(x)]-x的所有零点,可得$4{x}^{2}-5x+1=0,x∈[0,\frac{1}{2})$,解得x=$\frac{1}{4}$;
3x-2=0,x$∈[\frac{1}{2},\frac{3}{4})$,解得x=$\frac{2}{3}$,
$-2{(-2x+\frac{3}{2})}^{2}+1-x=0;x∈[\frac{3}{4},1]$,解得x=$\frac{7}{8}$.
函数y=f[f(x)]-x的所有零点之和为:$\frac{43}{24}$.
点评 本题考查分段函数的应用,函数的零点的求法,考查计算能力.

 走进文言文系列答案
走进文言文系列答案| A. | 有且只有一个 | B. | 有且只有两个 | C. | 有且只有三个 | D. | 有且只有四个 |
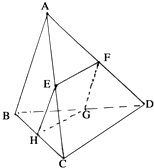 如图所示,四边形EFGH为四面体ABCD的一个截面,若四边形EFGH为平行四边形.
如图所示,四边形EFGH为四面体ABCD的一个截面,若四边形EFGH为平行四边形.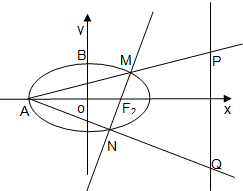 如图所示,设F1、F2是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点,A、B分别为其左顶点与上顶点,椭圆的离心率e=$\frac{1}{2}$,原点到过点A、B的直线的距离为$\frac{{2\sqrt{21}}}{7}$.
如图所示,设F1、F2是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点,A、B分别为其左顶点与上顶点,椭圆的离心率e=$\frac{1}{2}$,原点到过点A、B的直线的距离为$\frac{{2\sqrt{21}}}{7}$.