题目内容
18.(1)已知椭圆中心在原点,焦点在坐标轴上,长轴长为短轴长的2倍,且过点P(4,2),求此椭圆的方程;(2)求与双曲线$\frac{{x}^{2}}{5}-\frac{{y}^{2}}{3}$=1有公共渐近线,且焦距为8的双曲线的方程.
分析 (1)分类讨论,设出椭圆的方程,代入点(4,2)解得b2,即可求此椭圆的方程;
(2)与双曲线$\frac{{x}^{2}}{5}-\frac{{y}^{2}}{3}$=1有公共渐近线,可设为$\frac{{x}^{2}}{5}-\frac{{y}^{2}}{3}$=λ,即为$\frac{{x}^{2}}{5λ}$-$\frac{{y}^{2}}{3λ}$=1,分类讨论,利用焦距为8,即可求出双曲线的方程.
解答 解:(1)由已知a=2b,当焦点在x轴上时,椭圆方程为$\frac{{x}^{2}}{4{b}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,代入点(4,2)解得b2=8,此时椭圆方程为$\frac{{x}^{2}}{32}$+$\frac{{y}^{2}}{8}$=1.
当焦点在y轴上时,椭圆方程为$\frac{{y}^{2}}{4{b}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1,代入点(4,2)解得b2=17,此时椭圆方程为$\frac{{x}^{2}}{17}$+$\frac{{y}^{2}}{68}$=1.…(6分)
(2)与双曲线$\frac{{x}^{2}}{5}-\frac{{y}^{2}}{3}$=1有公共渐近线的双曲线可设为$\frac{{x}^{2}}{5}-\frac{{y}^{2}}{3}$=λ,即为$\frac{{x}^{2}}{5λ}$-$\frac{{y}^{2}}{3λ}$=1.
当焦点在x轴上时,λ>0,2$\sqrt{5λ+3λ}$=8,λ=2,此时双曲线为$\frac{{x}^{2}}{10}-\frac{{y}^{2}}{6}$=1.
当焦点在y轴上时,λ<0,2$\sqrt{-5λ-3λ}$=8,λ=-2,此时双曲线为$\frac{{x}^{2}}{10}-\frac{{y}^{2}}{6}$=-1.…(12分)
点评 本题考查椭圆、双曲线的方程与性质,考查分类讨论的数学思想,属于中档题.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案| A. | 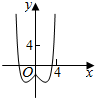 | B. | 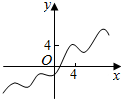 | C. | 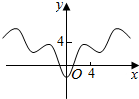 | D. | 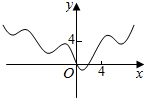 |
| A. | 甲地:总体均值为6,中位数为8 | B. | 乙地:总体均值为5,方差为12 | ||
| C. | 丙地:中位数为5,众数为6 | D. | 丁地:总体均值为3,方差大于0 |
| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{\sqrt{10}}{2}$ | D. | $\sqrt{6}$ |