题目内容
已知数列{a}的前n项和为Sn,且Sn=n2+3n+2,n∈N×(I)求{an}的通项公式;
(II)2bn=bn-1+an(n≥2,n∈N×)确定的数列{bn}能否为等差数列?若能,求b1的值;若不能,说明理由.
分析:(I)先看当n=1时利用a1=S1,求得a1.进而当n≥2时根据an=Sn-Sn-1求得an,最后综合可求得数列{an}的通项公式.
(II)把(I)中求得的代an入2bn=bn-1+an中求得数列的递推式,进而利用累乘法求得bn-2n=(b1-2)(
)n-1进而分别看b1=2和b1≠2求得bn,进而可得结论.
(II)把(I)中求得的代an入2bn=bn-1+an中求得数列的递推式,进而利用累乘法求得bn-2n=(b1-2)(
| 1 |
| 2 |
解答:解:(I)n=1时,a1=S1=6,
当n≥2时,an=Sn-Sn-1=2n+2
所以{an}的通项公式为an=
(II)由(I)知当n≥2时,2bn=bn-1+2n+2,
整理得:bn-2n=
[bn-1-2(n-1)]
利用累乘法得:bn-2n=(b1-2)(
)n-1
若b1=2,则bn=2n,{bn}为等差数列;
若b1≠2,则bn=2n+(b1-2)(
)n-1,此时{bn}不是等差数列
所以当b1=2时,数列{bn}为等差数列.
当n≥2时,an=Sn-Sn-1=2n+2
所以{an}的通项公式为an=
|
(II)由(I)知当n≥2时,2bn=bn-1+2n+2,
整理得:bn-2n=
| 1 |
| 2 |
利用累乘法得:bn-2n=(b1-2)(
| 1 |
| 2 |
若b1=2,则bn=2n,{bn}为等差数列;
若b1≠2,则bn=2n+(b1-2)(
| 1 |
| 2 |
所以当b1=2时,数列{bn}为等差数列.
点评:本题主要考查了等差关系的确定.常涉及等差数列的通项公式和求和公式,考查了学生的基础知识的掌握.

练习册系列答案
相关题目
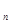 }的前n项和Sn= —a
}的前n项和Sn= —a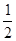 )
)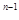 +2
(n为正整数).
+2
(n为正整数).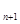 =
= .,并求数列{a
.,并求数列{a =
=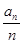 ,T
,T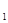 +c
+c +···+c
+···+c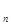 .
.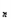 }的前n项和Sn= -a
}的前n项和Sn= -a -(
-( )
) +2 (n为正整数).
+2 (n为正整数).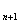 =
= a
a + (
+ (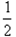 )
) .,并求数列{a
.,并求数列{a }的通项
}的通项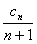 =
= ,T
,T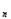 = c
= c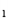 +c
+c +···+c
+···+c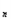 ,求T
,求T .
.