题目内容
已知数列{a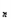 }的前n项和Sn= -a
}的前n项和Sn= -a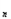 -(
-( )
) +2 (n为正整数).
+2 (n为正整数).
(1)证明:a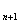 =
= a
a + (
+ (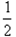 )
) .,并求数列{a
.,并求数列{a }的通项
}的通项
(2)若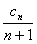 =
= ,T
,T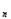 = c
= c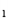 +c
+c +···+c
+···+c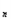 ,求T
,求T .
.
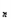 }的前n项和Sn= -a
}的前n项和Sn= -a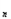 -(
-( )
) +2 (n为正整数).
+2 (n为正整数).(1)证明:a
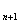 =
= a
a + (
+ (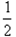 )
) .,并求数列{a
.,并求数列{a }的通项
}的通项(2)若
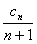 =
= ,T
,T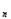 = c
= c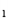 +c
+c +···+c
+···+c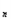 ,求T
,求T .
.解:(1)由S = -an- (
= -an- ( )
) +2,得S
+2,得S = -a
= -a -(
-( )
) +2,
+2,
两式相减,得a =-a
=-a + a
+ a +(
+( )
) ,即a
,即a =
= a
a +(
+( )
)

因为S = -a
= -a -(
-( )
) +2,令n=1,得a
+2,令n=1,得a =
= .
.
对于a =
= a
a +(
+( )
)
 ,两端同时除以(
,两端同时除以( )
)
 ,得2
,得2 a
a =2
=2 a
a +1,
+1,
即数列{2 a
a }是首项为2
}是首项为2 ·a
·a =1,公差为1的等差数列,
=1,公差为1的等差数列,
故2 a
a =n,所以a
=n,所以a =
=
(2)由(1)及 =
= ,得c
,得c = (n+1)(
= (n+1)( )
) ,
,
所以T =2×
=2× +3×(
+3×( )
) +4×(
+4×( )
) +···+(n+1) (
+···+(n+1) ( )
) ,①
,①
 T
T =2×(
=2×( )
) +3×(
+3×( )
) +4×(
+4×( )
) +···+(n+1) (
+···+(n+1) ( )
) ,②
,②
由①-②,得 T
T =1+(
=1+( )
) +(
+( )
) +···+(
+···+( )
) -(n+1) (
-(n+1) ( )
)
=1+ - (n+1) (
- (n+1) ( )
) =
= -
- .
.
所以T =3-
=3- .
.
 = -an- (
= -an- ( )
) +2,得S
+2,得S = -a
= -a -(
-( )
) +2,
+2,两式相减,得a
 =-a
=-a + a
+ a +(
+( )
) ,即a
,即a =
= a
a +(
+( )
)

因为S
 = -a
= -a -(
-( )
) +2,令n=1,得a
+2,令n=1,得a =
= .
.对于a
 =
= a
a +(
+( )
)
 ,两端同时除以(
,两端同时除以( )
)
 ,得2
,得2 a
a =2
=2 a
a +1,
+1,即数列{2
 a
a }是首项为2
}是首项为2 ·a
·a =1,公差为1的等差数列,
=1,公差为1的等差数列,故2
 a
a =n,所以a
=n,所以a =
=
(2)由(1)及
 =
= ,得c
,得c = (n+1)(
= (n+1)( )
) ,
, 所以T
 =2×
=2× +3×(
+3×( )
) +4×(
+4×( )
) +···+(n+1) (
+···+(n+1) ( )
) ,①
,① T
T =2×(
=2×( )
) +3×(
+3×( )
) +4×(
+4×( )
) +···+(n+1) (
+···+(n+1) ( )
) ,②
,② 由①-②,得
 T
T =1+(
=1+( )
) +(
+( )
) +···+(
+···+( )
) -(n+1) (
-(n+1) ( )
)
=1+
 - (n+1) (
- (n+1) ( )
) =
= -
- .
. 所以T
 =3-
=3- .
.
练习册系列答案
相关题目
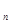 }的前n项和Sn= —a
}的前n项和Sn= —a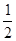 )
)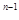 +2
(n为正整数).
+2
(n为正整数).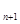 =
= .,并求数列{a
.,并求数列{a =
=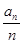 ,T
,T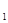 +c
+c +···+c
+···+c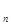 .
.