题目内容
已知两个等比数列{an}，{bn}，满足a1=a（a＞0），b1-a1=1，b2-a2=2，b3-a3=3，
（1）若a=1，求数列{an}的通项公式；
（2）若数列{an}唯一，求a的值。
（1）若a=1，求数列{an}的通项公式；
（2）若数列{an}唯一，求a的值。
解：（1）当a=1时，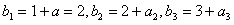
，
又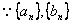
为等比数列，不妨设
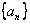的公比为q1，
由等比数列性质知：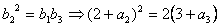
，
同时又有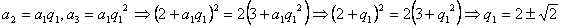
，
所以，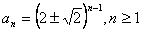
；
（2）{an}要唯一，∴当公比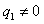
时，
由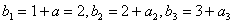
且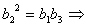
，
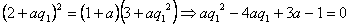∵a＞0，
∴
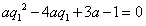最少有一个根（有两个根时，保证仅有一个正根），
∴
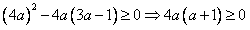，此时满足条件的a有无数多个，不符合；
∴当公比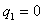
时，等比数列{an}首项为a，其余各项均为常数0，唯一，
此时由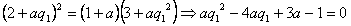
，可推得3a-1=0，
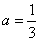符合；
综上，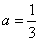
。
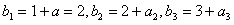，又
为等比数列，不妨设的公比为q1，由等比数列性质知：
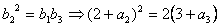，同时又有
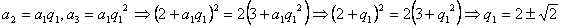，所以，
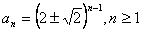；（2）{an}要唯一，∴当公比
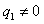时，由
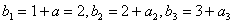
且
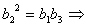
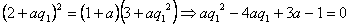，∵a＞0，
∴
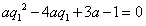最少有一个根（有两个根时，保证仅有一个正根），∴
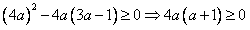，此时满足条件的a有无数多个，不符合；∴当公比
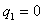时，等比数列{an}首项为a，其余各项均为常数0，唯一，此时由
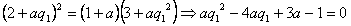，可推得3a-1=0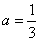，符合；综上，
。 
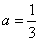练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目