题目内容
已知数列{an};an+1=-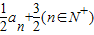 且a1=4,其前n项之和为Sn,则满足不等式|Sn-n-2|<
且a1=4,其前n项之和为Sn,则满足不等式|Sn-n-2|<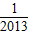 的最小整数n是 .
的最小整数n是 .
【答案】分析:由an+1=- ,得
,得 ,从而可知{an-1}为首项是3,公比为-
,从而可知{an-1}为首项是3,公比为- 的等比数列,
的等比数列,
由此可求得an,进而得到Sn,解不等式可得答案.
解答:解:由an+1=- ,得
,得 ,
,
又a1=4,所以{an-1}为首项是3,公比为- 的等比数列,
的等比数列,
则an-1= ,an=1+
,an=1+ ,
,
所以Sn=n+3• =n+2-2
=n+2-2 ,
,
则|Sn-n-2|= ,|Sn-n-2|<
,|Sn-n-2|< ,即
,即 ,解得n>11,
,解得n>11,
满足不等式|Sn-n-2|< 的最小整数n是12,
的最小整数n是12,
故答案为:12.
点评:本题考查由递推式求数列通项、数列求和及不等式等有关知识,解决本题的关键是通过构造数列求得an.
 ,得
,得 ,从而可知{an-1}为首项是3,公比为-
,从而可知{an-1}为首项是3,公比为- 的等比数列,
的等比数列,由此可求得an,进而得到Sn,解不等式可得答案.
解答:解:由an+1=-
 ,得
,得 ,
,又a1=4,所以{an-1}为首项是3,公比为-
 的等比数列,
的等比数列,则an-1=
 ,an=1+
,an=1+ ,
,所以Sn=n+3•
 =n+2-2
=n+2-2 ,
,则|Sn-n-2|=
 ,|Sn-n-2|<
,|Sn-n-2|< ,即
,即 ,解得n>11,
,解得n>11,满足不等式|Sn-n-2|<
 的最小整数n是12,
的最小整数n是12,故答案为:12.
点评:本题考查由递推式求数列通项、数列求和及不等式等有关知识,解决本题的关键是通过构造数列求得an.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目