题目内容
设函数
（
）
（1）求曲线
在点(0,f(0))处的切线方程；w.w.w.k.s.5.u.c.o.m
（2）求函数的单调区间;
（3）若函数
在区间(-1,1)内单调递增，求
的取值范围
⑴因为
，
，所以曲线
在点
处的切线方程为
；
⑵
，由
得
若
，则当
时，
，函数
单调递减；
当
时，
，函数
单调递增；
若
，则当时，，函数单调递增；；
当时，，函数单调递减
⑶由⑵知，若，则当且仅当
，即
时，函数在区间
内单调递增；
若，则当且仅当
，即
时，函数在区间内单调递增；
综上所述，函数在区间内单调递增时，
的取值范围为
.
解析:
⑴利用导数的几何意义可求函数
在点(0,f(0))处的切线方程；
⑵利用导数的正负求出函数的单调区间；⑶函数在区间(-1,1)内单调递增，说明
在区间(-1,1)内恒成立.
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
，其中
的单调区间；
时，证明不等式
；
，若存在实数
使得
，则称函数
存在零点
内有零点。
且
）
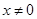的单调区间；
对任意
恒成立，求实数
的取值范围。
，其中
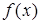的最小正周期和单调递减区间；
在[
上最大值与最小值.
，
。
的单调区间和极值。
的方程
时，
恒成立，求实数
的取值范围。
（常数
的定义域；
满足什么条件时，
在
上恒取正值。