题目内容
已知△ABC的三边长分别为a，b，c，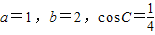
，（1）求△ABC的周长；
（2）求△ABC的面积．
【答案】分析：（1）△ABC中，有余弦定理求得c的值，即可求得△ABC的周长．
（2）由cosC=
，利用同角三角函数的基本关系求得 sinC=
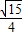，再根据△ABC的面积为 
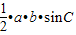，运算求得结果．
解答：解：（1）△ABC中，∵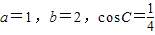
，∴c2=a2+b2-2ab•cosC=4，∴c=2．
∴△ABC的周长为 a+b+c=5．
（2）∵cosC=
，∴sinC=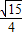
，
∴△ABC的面积为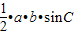
=
．
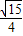点评：本题主要考查正弦定理和余弦定理的应用，同角三角函数的基本关系，已知三角函数值求角的大小，属于中档题．
（2）由cosC=
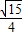，利用同角三角函数的基本关系求得 sinC=，再根据△ABC的面积为 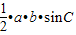，运算求得结果．解答：解：（1）△ABC中，∵
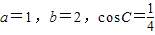，∴c2=a2+b2-2ab•cosC=4，∴c=2．∴△ABC的周长为 a+b+c=5．
（2）∵cosC=
，∴sinC=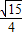，∴△ABC的面积为
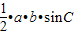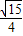=．点评：本题主要考查正弦定理和余弦定理的应用，同角三角函数的基本关系，已知三角函数值求角的大小，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知△ABC的三边长为a、b、c，满足直线ax+by+c=0与圆x2+y2=1相离，则△ABC是（ ）
| A、锐角三角形 | B、直角三角形 | C、钝角三角形 | D、以上情况都有可能 |