题目内容
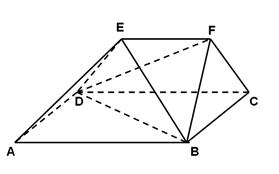
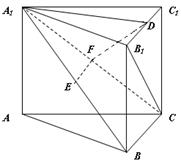
(本小题满分14分) 如图3所示,四棱锥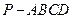 中,底面
中,底面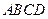 为正方形,
为正方形, 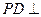 平面
平面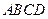 ,
,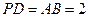 ,
,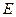 ,
,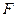 ,
,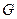 分别为
分别为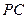 、
、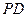 、
、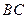 的中点.
的中点.
(1)求证: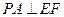 ;
;
(2)求二面角D-FG-E的余弦值.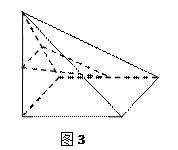
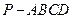 中,底面
中,底面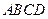 为正方形,
为正方形, 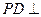 平面
平面 ,
,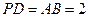 ,
,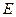 ,
,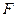 ,
,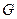 分别为
分别为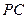 、
、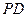 、
、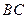 的中点.
的中点.(1)求证:
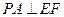 ;
;(2)求二面角D-FG-E的余弦值.

(1)证明略;
(2)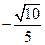
(2)
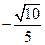
(1)证法1:∵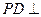 平面
平面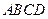 ,
,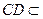 平面
平面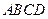 ,∴
,∴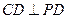 .
.
又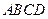 为正方形,∴
为正方形,∴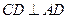 .
.
∵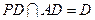 ,∴
,∴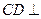 平面
平面 .……………………………………………3分
.……………………………………………3分
∵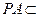 平面
平面 ,∴
,∴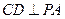 .
.
∵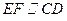 ,∴
,∴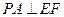 .…………………………………………………………6分
.…………………………………………………………6分
证法2:以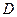 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系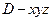 ,则
,则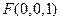 ,
,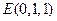
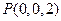 ,
,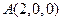 ,
,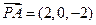 ,
,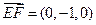 .………4分
.………4分
∵ ,∴
,∴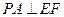 .………6分
.………6分

(2)解法1:以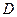 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系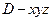 ,
,
则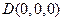 ,
,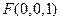 ,
,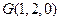 ,
,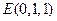 ,
,
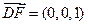 ,
,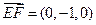 ,……………8分
,……………8分
设平面DFG的法向量为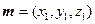 ,
,
∵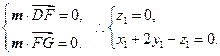
令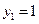 ,得
,得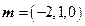 是平面
是平面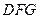 的一个法向量.…………………………10分
的一个法向量.…………………………10分
设平面EFG的法向量为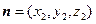 ,
,
∵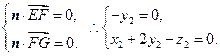
令 ,得
,得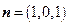 是平面
是平面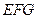 的一个法向量.……………………………12分
的一个法向量.……………………………12分
∵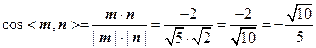 .
.
设二面角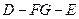 的平面角为θ,则
的平面角为θ,则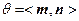 .
.
所以二面角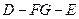 的余弦值为
的余弦值为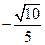 .………………………………………14分
.………………………………………14分
解法2:以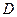 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系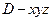 ,W
,W
则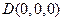 ,
,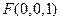 ,
,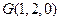 ,
,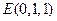 ,
,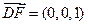 ,
,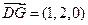
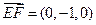 ,
,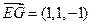 ,
,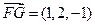 .………………………………8分
.………………………………8分
过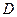 作
作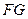 的垂线,垂足为
的垂线,垂足为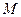 ,
,
∵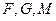 三点共线,∴
三点共线,∴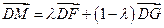 ,
,
∵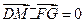 ,∴
,∴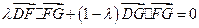 ,
,
即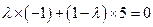 ,解得
,解得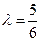 .
.
∴ .………………………………………………10分
.………………………………………………10分
再过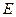 作
作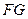 的垂线,垂足为
的垂线,垂足为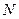 ,
,
∵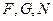 三点共线,∴
三点共线,∴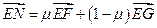 ,
,
∵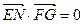 ,∴
,∴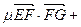
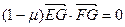 ,
,
即 ,解得
,解得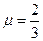 .
.
∴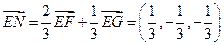 .……………………………………………12分
.……………………………………………12分
∴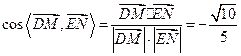 .
.
∵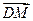 与
与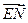 所成的角就是二面角
所成的角就是二面角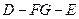 的平面角,
的平面角,
所以二面角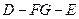 的余弦值为
的余弦值为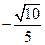 .………………………………………14分
.………………………………………14分

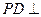 平面
平面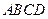 ,
,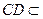 平面
平面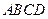 ,∴
,∴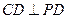 .
.又
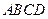 为正方形,∴
为正方形,∴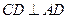 .
.∵
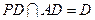 ,∴
,∴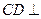 平面
平面 .……………………………………………3分
.……………………………………………3分∵
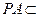 平面
平面 ,∴
,∴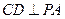 .
.∵
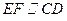 ,∴
,∴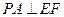 .…………………………………………………………6分
.…………………………………………………………6分证法2:以
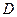 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系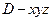 ,则
,则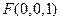 ,
,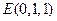
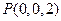 ,
,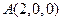 ,
,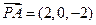 ,
,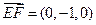 .………4分
.………4分∵
 ,∴
,∴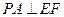 .………6分
.………6分
(2)解法1:以
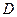 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系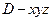 ,
,则
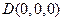 ,
,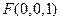 ,
,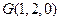 ,
,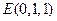 ,
, 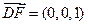 ,
,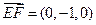 ,……………8分
,……………8分设平面DFG的法向量为
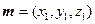 ,
,∵
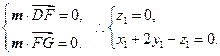
令
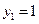 ,得
,得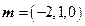 是平面
是平面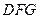 的一个法向量.…………………………10分
的一个法向量.…………………………10分设平面EFG的法向量为
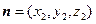 ,
,∵
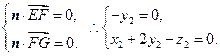
令
 ,得
,得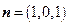 是平面
是平面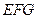 的一个法向量.……………………………12分
的一个法向量.……………………………12分∵
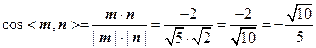 .
.设二面角
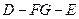 的平面角为θ,则
的平面角为θ,则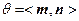 .
.所以二面角
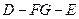 的余弦值为
的余弦值为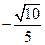 .………………………………………14分
.………………………………………14分解法2:以
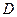 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系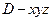 ,W
,W则
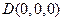 ,
,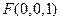 ,
,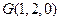 ,
,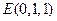 ,
,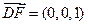 ,
,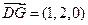
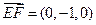 ,
,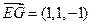 ,
,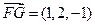 .………………………………8分
.………………………………8分过
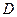 作
作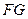 的垂线,垂足为
的垂线,垂足为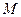 ,
,∵
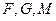 三点共线,∴
三点共线,∴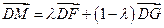 ,
,∵
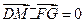 ,∴
,∴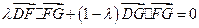 ,
,即
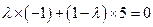 ,解得
,解得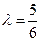 .
.∴
 .………………………………………………10分
.………………………………………………10分再过
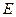 作
作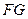 的垂线,垂足为
的垂线,垂足为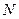 ,
,∵
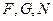 三点共线,∴
三点共线,∴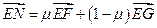 ,
,∵
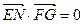 ,∴
,∴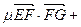
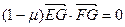 ,
,即
 ,解得
,解得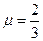 .
.∴
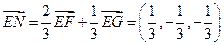 .……………………………………………12分
.……………………………………………12分∴
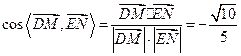 .
.∵
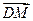 与
与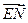 所成的角就是二面角
所成的角就是二面角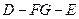 的平面角,
的平面角,所以二面角
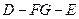 的余弦值为
的余弦值为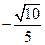 .………………………………………14分
.………………………………………14分

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
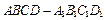 中,点
中,点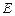 在棱
在棱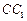 的延长线上,且
的延长线上,且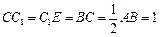 .
.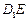 ∥平面
∥平面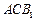 ;
;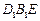
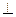 平面
平面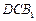 ;
;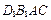 的体积.
的体积.
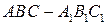 中,
中, 分别是
分别是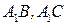 的中点,点
的中点,点
 在
在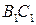 上,
上,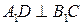
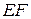 ∥平面
∥平面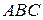
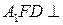 平面
平面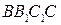
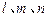 及平面
及平面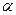 ,下列命题中的假命题是 ( )
,下列命题中的假命题是 ( )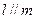 ,
,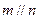 ,则
,则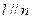
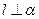 ,
,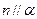 ,则
,则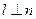
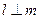 ,
,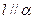 ,
, 在底半径为
在底半径为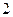 ,高为
,高为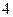 的圆锥中内接一个的圆柱,圆柱的最大侧面积为_______
的圆锥中内接一个的圆柱,圆柱的最大侧面积为_______

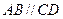 ,
,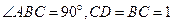 ,AB=2,E为AB的中点,将
,AB=2,E为AB的中点,将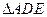 沿DE翻折至
沿DE翻折至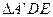 ,使二面角A
,使二面角A
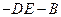 为直二面角。
为直二面角。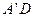 、
、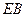 的中点,求证:
的中点,求证: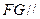 平面
平面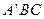 ;
;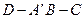 度数的余弦值
度数的余弦值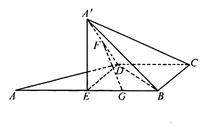
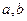 是两条不同的直线,
是两条不同的直线,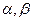 是两个不重合的平面,则下列命题中正确的是 ( )
是两个不重合的平面,则下列命题中正确的是 ( )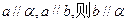
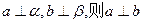
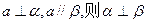
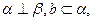 则
则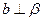
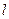 及两个平面
及两个平面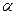 、
、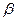 ,下列命题正确的是 ( )
,下列命题正确的是 ( )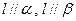 ,则
,则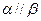
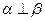
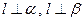 , 则
, 则