题目内容
函数y=ax(a>1)的定义域是[-1,1],且最大值与最小值的差为1,则a=________.

分析:由y=ax(a>1)在[-1,1]上是增函数,知ymax=a,
 ,由最大值与最小值的差为1,知
,由最大值与最小值的差为1,知 =1,由此能求出a的值.
=1,由此能求出a的值.解答:∵y=ax(a>1)在[-1,1]上是增函数,
∴ymax=a,
 ,
,∵最大值与最小值的差为1,
∴
 =1,
=1,∴a2-a-1=0,
∴
 ,
,∵a>1,
∴a=
 .
.故答案为:
 .
.点评:本题考查指数函数的单调性的应用,是基础题,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
已知函数y=ax(a>1)在区间[1,2]上的最大值与最小值之差为2,则实数a的值为( )
A、
| ||
| B、2 | ||
| C、3 | ||
| D、4 |
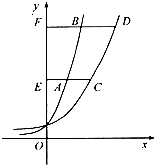 如图,A,B是函数y=ax(a>1)在y轴右侧图象上的两点,分别过A,B作y轴的垂线与y轴交于E,F两点,与函数y=ex的图象交于C,D两点,且A是CE的中点.
如图,A,B是函数y=ax(a>1)在y轴右侧图象上的两点,分别过A,B作y轴的垂线与y轴交于E,F两点,与函数y=ex的图象交于C,D两点,且A是CE的中点.