题目内容
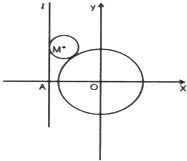已知直线l：x=m（m＜-2）与x轴交于A点，动圆M与直线l相切，并且和圆O：x2+y2=4相外切．（1）求动圆圆心M的轨迹C的方程．
（2）若过原点且倾斜角为
| π | 3 |
分析：（1）设出动圆圆心坐标，由动圆圆心到切线的距离等于动圆与定圆的圆心距减定圆的半径列式求解动圆圆心的轨迹方程；
（2）求出过原点且倾斜角为
的直线方程，和曲线C联立后利用根与系数关系得到M，N的横纵坐标的和与积，由
•
=0列式求解m的值．
（2）求出过原点且倾斜角为
| π |
| 3 |
| AM |
| AN |
解答：解：（1）设动圆的圆心M坐标（x0，y0），
∵动圆M与直线l相切，并且和圆O：x2+y2=4相外切，
∴|x0-m|=
-2，即x0+2-m=
．
整理得：y02=(4-2m)x0+(2-m)2．
∴动圆圆心M的轨迹C的方程为y2=（4-2m）x+（2-m）2．
（2）存在以MN为直径的圆过点A．
事实上，过原点倾斜角为
的直线方程为y=
x．
联立
，得3x2-（4-2m）x-（2-m）2=0．
设M（x1，y1），N（x2，y2），
则x1+x2=
，x1x2=
，
y1y2=3x1x2=m2-2．
若存在以MN为直径的圆过点A，则
•
=0，
即（x1+m，y1）•（x2+m，y2）
=x1x2+m(x1+x2)+m2+y1y2
=
+m•
+m2+m2-2
=
=0，解得：m=
或m=
（舍）．
∴存在以MN为直径的圆过点A，此时m=
．
∵动圆M与直线l相切，并且和圆O：x2+y2=4相外切，
∴|x0-m|=
| x02+y02 |
| x02+y02 |
整理得：y02=(4-2m)x0+(2-m)2．
∴动圆圆心M的轨迹C的方程为y2=（4-2m）x+（2-m）2．
（2）存在以MN为直径的圆过点A．
事实上，过原点倾斜角为
| π |
| 3 |
| 3 |
联立
|
设M（x1，y1），N（x2，y2），
则x1+x2=
| 4-2m |
| 3 |
| m2-2 |
| 3 |
y1y2=3x1x2=m2-2．
若存在以MN为直径的圆过点A，则
| AM |
| AN |
即（x1+m，y1）•（x2+m，y2）
=x1x2+m(x1+x2)+m2+y1y2
=
| m2-2 |
| 3 |
| 4-2m |
| 3 |
=
| 5m2+4m-8 |
| 3 |
-2-
| ||
| 5 |
-2+
| ||
| 5 |
∴存在以MN为直径的圆过点A，此时m=
-2-
| ||
| 5 |
点评：本题考查了轨迹方程的求法，考查了直线与圆锥曲线的关系，训练了利用数量积判断两个向量的垂直关系，考查了学生的计算能力，是有一定难度题目．
练习册系列答案
相关题目
的直线与曲线
的直线与曲线