题目内容
函数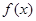 的导函数为
的导函数为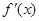 ,若对于定义域内任意
,若对于定义域内任意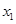 ,
,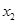
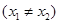 ,有
,有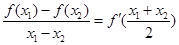 恒成立,则称
恒成立,则称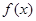 为恒均变函数.给出下列函数:①
为恒均变函数.给出下列函数:①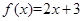 ;②
;②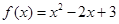 ;③
;③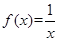 ;④
;④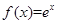 ;⑤
;⑤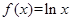 .其中为恒均变函数的序号是 .(写出所有满足条件的函数的序号)
.其中为恒均变函数的序号是 .(写出所有满足条件的函数的序号)
①②
解析试题分析:对于①f(x)=2x+3, 满足
满足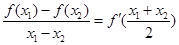 ,为恒均变函数;对于②f(x)=x2-2x+3,
,为恒均变函数;对于②f(x)=x2-2x+3, ,
, ,故满足
,故满足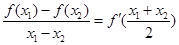 ,为恒均变函数;
,为恒均变函数;
对于;③f(x)= ,
, ,显然不满足
,显然不满足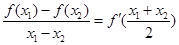 ,故不是恒均变函数;对于④f(x)=ex ,
,故不是恒均变函数;对于④f(x)=ex , ,显然不满足
,显然不满足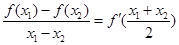 ,故不是恒均变函数;对于⑤f(x)=lnx,
,故不是恒均变函数;对于⑤f(x)=lnx, ,显然不满足
,显然不满足 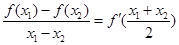 ,故不是恒均变函数.故应填入: ①②.
,故不是恒均变函数.故应填入: ①②.
考点:1.函数的导数运算;2.判断命题的真假.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数 的导函数是
的导函数是 ,集合
,集合 ,若
,若 ,则 ( )
,则 ( )
A. | B. |
C. | D. |
函数 存在与直线
存在与直线 平行的切线,则实数
平行的切线,则实数 的取值范围是( )
的取值范围是( )
A. | B. |
C. | D. |
 和直线
和直线 相切,则
相切,则  .
. ,则
,则 =____________。
=____________。 ,
, ,…,
,…,
 .
. ,则
,则 的值为 .
的值为 .  的不等式
的不等式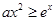 的解集中的正整数解有且只有3个,则实数
的解集中的正整数解有且只有3个,则实数 的取值范围是 .
的取值范围是 . 在
在 处的切线的斜率为 .
处的切线的斜率为 .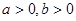 ,且函数
,且函数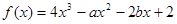 在
在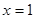 处有极值,则ab的最大值为 .
处有极值,则ab的最大值为 .