题目内容
函数
(Ⅰ)判断并证明函数的奇偶性;
(Ⅱ)若a=2,证明函数f(x)在(2,+∞)上单调递增;
(Ⅲ)在满足(Ⅱ)的条件下,解不等式f(t2+2)+f(-2t2+4t-5)<0.
(I)解:该函数为奇函数.
证明:函数的定义域为(-∞,0)∪(0,+∞)关于原点对称,
且f(-x)=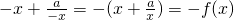 ,
,
故函数f(x)为奇函数.
(II)当a=2时,f(x)= .
.
?2<x1<x2,
则f(x1)-f(x2)=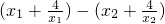 =
=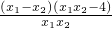 .
.
∵2<x1<x2,∴x1-x2<0,x1x2>4,即x1x2-4>0.
∴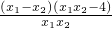 <0,
<0,
∴f(x1)<f(x2),函数f(x)在(2,+∞)上单调递增.
(III)∵f(x)为奇函数,∴f(t2+2)<-f(-2t2+4t-5)=f(2(t-1)2+3),
∵t2+2≥2,2(t-1)2+3>2,函数f(x)在(2,+∞)上单调递增,
∴t2+2<2t2-4+5,
化为t2-4t+3>0,解得t<1或t>3.
分析:(I)利用奇函数的定义即可判断出;
(II)利用函数的单调性的定义即可证明;
(III)利用奇函数的性质和单调性即可解出.
点评:熟练掌握奇函数的性质和单调性是解题的关键.
证明:函数的定义域为(-∞,0)∪(0,+∞)关于原点对称,
且f(-x)=
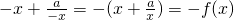 ,
,故函数f(x)为奇函数.
(II)当a=2时,f(x)=
 .
.?2<x1<x2,
则f(x1)-f(x2)=
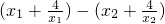 =
=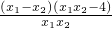 .
.∵2<x1<x2,∴x1-x2<0,x1x2>4,即x1x2-4>0.
∴
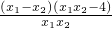 <0,
<0,∴f(x1)<f(x2),函数f(x)在(2,+∞)上单调递增.
(III)∵f(x)为奇函数,∴f(t2+2)<-f(-2t2+4t-5)=f(2(t-1)2+3),
∵t2+2≥2,2(t-1)2+3>2,函数f(x)在(2,+∞)上单调递增,
∴t2+2<2t2-4+5,
化为t2-4t+3>0,解得t<1或t>3.
分析:(I)利用奇函数的定义即可判断出;
(II)利用函数的单调性的定义即可证明;
(III)利用奇函数的性质和单调性即可解出.
点评:熟练掌握奇函数的性质和单调性是解题的关键.

练习册系列答案
相关题目
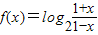 .
.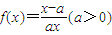
 .
.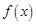 的奇偶性;
的奇偶性;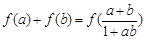 ;
; ,
, ,求
,求 ,
, 的值.
的值.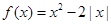 .
.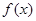 的图像指出其在
的图像指出其在 上的单调性.
上的单调性.