Question

已知圆C:.

(1)直线过点P(1,2)，且与圆C交于A、B两点，若，求直线的方程；

(2)过圆C上一动点M作平行于y轴的直线m，设m与x轴的交点为N，若向量，求动点的轨迹方程.

(3) 若点R(1,0)，在（2）的条件下，求的最小值.

Answer 1

(1) 所求直线为3x-4y+5=0或x=1  (2) 点的轨迹方程是  () (3)

解析:

（1）①当直线垂直于轴时，则此时直线方程为，与圆的两个交点坐标为

和，其距离为，满足题意                        ………1分

②若直线不垂直于轴，设其方程为，即 ………2分

设圆心到此直线的距离为，则，得∴，，………4分

故所求直线方程为3x-4y+5=0   

综上所述，所求直线为3x-4y+5=0或x=1                           ……………5分

(2)设点M的坐标为(x₀,y₀)，Q点坐标为(x,y)则N点坐标是(x₀, 0)

   ∵，∴  即，    ………7分

又∵，∴                     …………9分

由已知，直线m //oy轴，所以，,

∴点的轨迹方程是  ()                ………………10分

（3）设Q坐标为(x,y)，， ， ………………11分

又  ()可得：

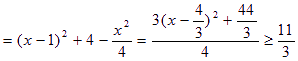.         ………………13分

         …………14分