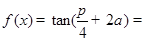题目内容
设α为第一象限的角, ,则
,则 = .
= .
【答案】分析:有条件求得cosα 和sinα的值,可得tanα 的值,再利用二倍角的正切公式求出 tan2α 的值,再利用两角和差的正切公式求出 的值.
的值.
解答:解:∵α为第一象限的角, ,
,
∴2cos2α-1=- ,解得 cosα=
,解得 cosα= ,sinα=
,sinα= ,故tanα=2.
,故tanα=2.
∴tan2α= =-
=- .
.
∴ =
= =-
=- ,
,
故答案为- .
.
点评:本题主要考查两角和差的正切公式、二倍角的正切公式的应用,属于中档题.
 的值.
的值.解答:解:∵α为第一象限的角,
 ,
,∴2cos2α-1=-
 ,解得 cosα=
,解得 cosα= ,sinα=
,sinα= ,故tanα=2.
,故tanα=2.∴tan2α=
 =-
=- .
.∴
 =
= =-
=- ,
,故答案为-
 .
.点评:本题主要考查两角和差的正切公式、二倍角的正切公式的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
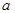 为第一象限的角,
为第一象限的角,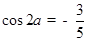 ,则
,则