题目内容
设等比数列{an}的前n项的和为Sn,积为Pn,各项倒数的前n项和为Tn.求证:Pn2=(
)n.
解析:本题考查等比数列的前n项和公式.
证明:设{an}的公比为q.
当q=1时,Sn=na1,Pn=a1n,Tn=,
∴(
)n=(na1·
)n=a12n=Pn2成立;
当q≠1时,Sn=
,
Pn=a1nq1+2+…+(n-1)=a1n·
,
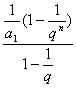Tn=
,
∴(
)n=［
·
］n
=(a12qn-1)n.
∴Pn2=a12n·qn(n-1)=(a12qn-1)n=(
)2.
综上,Pn2=(
)2.
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
相关题目
设等比数列{an}的前n项和为Sn，若8a2+a5=0，则下列式子中数值不能确定的是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设等比数列{an}的前n项和为Sn，若
=3，则
=（ ）
| S6 |
| S3 |
| S9 |
| S6 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |