题目内容
a,b,c∈R+,求证:a+b+c≤
+
+
≤
+
+
.
证明：不妨设a≥b≥c＞0,则≥≥,a2≥b2≥c2,?
则a2·+b2·+c2·≤
+
+
,a2·
+b2·
+c2·
≤
+
+
,两式相加得
a+b+c≤
+
+
.?
又a3≥b3≥c3,
≥
≥
＞0,?
∴
+
+
≥
+
+
=
+
+
,
+
+
≥
+
+
=
+
+
.
两式相加,得
+
+
≤
+
+
.?
即不等式成立.
温馨提示
排序不等式中注意排序原理中顺序和,乱序和的各种形式和条件.
练习册系列答案
星级口算天天练系列答案
相关题目
≥|
≥|
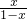|}，C={x|ax2+x+b＜0}，
，A∪B∪C=R，求实数a、b的值．
≥|
|}，C={x|ax2+x+b＜0}，