题目内容
设三棱锥S-ABC中,SA,SB,SC两两垂直,且SA=4,SB=3,SC=5,D是SA的中点,E是BC的中点,则三棱锥B-ADE的体积为
.
| 5 |
| 2 |
| 5 |
| 2 |
分析:据题意画出如下图形则三棱锥B-ADE的体积即为三棱锥D-ABE的体积又D是SA的中点,E是BC的中点则为三棱锥D-ABE的高为三棱锥S-ABC的高的一半且三角形ABE的面积为三角形ABC的面积的一半即三棱锥B-ADE的体积为三棱锥S-ABC体积的
而要求三棱锥S-ABC的体积可结合SA,SB,SC两两垂直轮换三棱锥S-ABC的顶点转化为求三棱锥A-SBC的体积而三棱锥A-SBC的体积比较容易求出.
| 1 |
| 4 |
解答: 解:设三棱锥S-ABC的高位h
解:设三棱锥S-ABC的高位h
∵D是SA的中点
∴三棱锥B-ADE的高为
h
∵E是BC的中点
∴S△ABE=
S△ABC
∴VB-ADE=VD-ABE=
×(
S△ABC)×(
h)=
VS-ABC=
VA-SCD
∵SA,SB,SC两两垂直
∴vA-SCB=
×
×3×5×4=10
∴VB-ADE=
× 10=
故答案为
 解:设三棱锥S-ABC的高位h
解:设三棱锥S-ABC的高位h∵D是SA的中点
∴三棱锥B-ADE的高为
| 1 |
| 2 |
∵E是BC的中点
∴S△ABE=
| 1 |
| 2 |
∴VB-ADE=VD-ABE=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∵SA,SB,SC两两垂直
∴vA-SCB=
| 1 |
| 3 |
| 1 |
| 2 |
∴VB-ADE=
| 1 |
| 4 |
| 5 |
| 2 |
故答案为
| 5 |
| 2 |
点评:本题主要考查了球三棱锥的体积.解题的关键是利用轮换三棱锥顶点的方法将三棱锥B-ADE的体积等价转化为三棱锥S-ABC体积的
而三棱锥S-ABC体积根据题中的条件很容易求出!
| 1 |
| 4 |

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC.
如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC.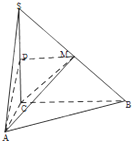 如图:在三棱锥S-ABC中,SC⊥平面ABC,点P,M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角60°
如图:在三棱锥S-ABC中,SC⊥平面ABC,点P,M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角60°