题目内容
设点E、F分别是椭圆C: (a>b>0)的左、右焦点,过点E垂直于椭圆长轴的直线交椭圆于A、B两点,△ABF是正三角形.
(a>b>0)的左、右焦点,过点E垂直于椭圆长轴的直线交椭圆于A、B两点,△ABF是正三角形.(1)求椭圆的离心率;
(2)设椭圆C的焦距为2,过点P(3,0)且不与坐标轴重合的直线交椭圆C于M、N两点,点M关于x轴的对称点为M',求证:直线M'N过x轴一定点,并求此定点坐标.

【答案】分析:(1)设椭圆的半焦距为c,则 直线AB的方程为x=-c,将x=-c代入椭圆方程,求得|AB|= ,|EF|=2c,根据△ABF是正三角形,可得
,|EF|=2c,根据△ABF是正三角形,可得 ,从而可求椭圆的离心率;
,从而可求椭圆的离心率;
(2)确定椭圆的方程为 ,设直线MN的方程为x=my+3代入椭圆方程,利用韦达定理及kQM=kQN,即可求导直线M'N过x轴一定点.
,设直线MN的方程为x=my+3代入椭圆方程,利用韦达定理及kQM=kQN,即可求导直线M'N过x轴一定点.
解答:解:(1)设椭圆的半焦距为c,则 直线AB的方程为x=-c,将x=-c代入椭圆方程 =1,注意到c2=a2-b2,解得y=±
=1,注意到c2=a2-b2,解得y=± ,所以|AB|=
,所以|AB|= ,|EF|=2c
,|EF|=2c
∵△ABF是正三角形,
∴
∴
∵ ,b2=a2-c2,
,b2=a2-c2,
∴ e2+2e-
e2+2e- =0
=0
∴ 或
或 (舍去)
(舍去)
故所求椭圆的离心率为
(2)由(1)知,a2=3c2,b2=2c2,∴椭圆的方程为 ,显然,直线l的斜率不为0
,显然,直线l的斜率不为0
因此,可设直线MN的方程为x=my+3代入椭圆方程可得(2m2+3)y2+12my+12=0
∵直线交椭圆C于M、N两点,∴△=48(m2-3)>0
设M(x1,y1),N(x2,y2),则M′(x1,-y1),
∴y1+y2=- ,y1y2=
,y1y2= ①
①
设直线M'N与x轴的交点为Q(t,0)
∵kQM=kQN,∴ =-
=-
∴t= ②
②
∵x1=my1+3,x2=my2+3③
将①③代入②得t= =3-2=1
=3-2=1
∴直线M'N过x轴一定点Q(1,0).
点评:本题考查椭圆的几何性质,考查椭圆的标准方程,解题的关键是确定几何量之间的关系,利用直线与椭圆联立,结合韦达定理求解.
 ,|EF|=2c,根据△ABF是正三角形,可得
,|EF|=2c,根据△ABF是正三角形,可得 ,从而可求椭圆的离心率;
,从而可求椭圆的离心率;(2)确定椭圆的方程为
 ,设直线MN的方程为x=my+3代入椭圆方程,利用韦达定理及kQM=kQN,即可求导直线M'N过x轴一定点.
,设直线MN的方程为x=my+3代入椭圆方程,利用韦达定理及kQM=kQN,即可求导直线M'N过x轴一定点.解答:解:(1)设椭圆的半焦距为c,则 直线AB的方程为x=-c,将x=-c代入椭圆方程
 =1,注意到c2=a2-b2,解得y=±
=1,注意到c2=a2-b2,解得y=± ,所以|AB|=
,所以|AB|= ,|EF|=2c
,|EF|=2c∵△ABF是正三角形,
∴

∴

∵
 ,b2=a2-c2,
,b2=a2-c2,∴
 e2+2e-
e2+2e- =0
=0∴
 或
或 (舍去)
(舍去)故所求椭圆的离心率为

(2)由(1)知,a2=3c2,b2=2c2,∴椭圆的方程为
 ,显然,直线l的斜率不为0
,显然,直线l的斜率不为0因此,可设直线MN的方程为x=my+3代入椭圆方程可得(2m2+3)y2+12my+12=0
∵直线交椭圆C于M、N两点,∴△=48(m2-3)>0
设M(x1,y1),N(x2,y2),则M′(x1,-y1),
∴y1+y2=-
 ,y1y2=
,y1y2= ①
①设直线M'N与x轴的交点为Q(t,0)
∵kQM=kQN,∴
 =-
=-
∴t=
 ②
②∵x1=my1+3,x2=my2+3③
将①③代入②得t=
 =3-2=1
=3-2=1∴直线M'N过x轴一定点Q(1,0).
点评:本题考查椭圆的几何性质,考查椭圆的标准方程,解题的关键是确定几何量之间的关系,利用直线与椭圆联立,结合韦达定理求解.

练习册系列答案
相关题目
 (2012•九江一模)设点E、F分别是椭圆C:
(2012•九江一模)设点E、F分别是椭圆C: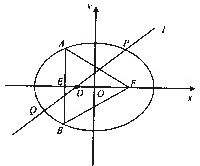 (2012•九江一模)设点E、F分别是椭圆C:
(2012•九江一模)设点E、F分别是椭圆C: 设点E、F分别是椭圆C:
设点E、F分别是椭圆C: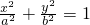 (a>b>0)的左、右焦点,过点E垂直于椭圆长轴的直线交椭圆于A、B两点,△ABF是正三角形.
(a>b>0)的左、右焦点,过点E垂直于椭圆长轴的直线交椭圆于A、B两点,△ABF是正三角形. 设点E、F分别是椭圆C:
设点E、F分别是椭圆C: =1(a>b>0)的左、右焦点,过点E垂直于椭圆长轴的直线交椭圆于A、B两点,△ABF是正三角形.
=1(a>b>0)的左、右焦点,过点E垂直于椭圆长轴的直线交椭圆于A、B两点,△ABF是正三角形. ,0)作直线l与椭圆C交于不同的两点P、Q,且满足
,0)作直线l与椭圆C交于不同的两点P、Q,且满足 ,O是坐标原点.当△OPQ的面积最大时,求椭圆的方程.
,O是坐标原点.当△OPQ的面积最大时,求椭圆的方程.