题目内容
求函数y= 的定义域和值域.
的定义域和值域.
解:由x2-5x+3≠0,
∴x≠ 且x≠
且x≠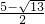 ,
,
∴函数y= 的定义域为:{x∈R|x≠
的定义域为:{x∈R|x≠ 且x≠
且x≠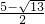 }.
}.
∵y= ,
,
∴yx2-(5y+1)x+3y-1=0,
当y=0时,x=-1,①
当y≠0时,上述方程有解,
∴△=[-(5y+1)]2-4y(3y-1)=13y2+14y+1≥0,
∴y≤-1或y≥- (y≠0)②.
(y≠0)②.
由①②可知,函数y= 的值域为:{y|y≤-1或y≥-
的值域为:{y|y≤-1或y≥- }.
}.
分析:由x2-5x+3≠0,可求得其定义域,将函数y= 化为方程yx2-(5y+1)x+3y-1=0,利用判别式法即可求得其值域.
化为方程yx2-(5y+1)x+3y-1=0,利用判别式法即可求得其值域.
点评:本题考查函数的定义域与值域的求法,着重考查判别式法求函数的值域,考查学生运算与灵活思维的能力,属于中档题.
∴x≠
 且x≠
且x≠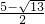 ,
,∴函数y=
 的定义域为:{x∈R|x≠
的定义域为:{x∈R|x≠ 且x≠
且x≠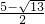 }.
}.∵y=
 ,
,∴yx2-(5y+1)x+3y-1=0,
当y=0时,x=-1,①
当y≠0时,上述方程有解,
∴△=[-(5y+1)]2-4y(3y-1)=13y2+14y+1≥0,
∴y≤-1或y≥-
 (y≠0)②.
(y≠0)②.由①②可知,函数y=
 的值域为:{y|y≤-1或y≥-
的值域为:{y|y≤-1或y≥- }.
}.分析:由x2-5x+3≠0,可求得其定义域,将函数y=
 化为方程yx2-(5y+1)x+3y-1=0,利用判别式法即可求得其值域.
化为方程yx2-(5y+1)x+3y-1=0,利用判别式法即可求得其值域.点评:本题考查函数的定义域与值域的求法,着重考查判别式法求函数的值域,考查学生运算与灵活思维的能力,属于中档题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 的定义域和值域
的定义域和值域 的定义域和值域.
的定义域和值域.