题目内容
5．
如图，在棱长为1的正方体ABCD-A1B1C1D1中，P为棱A1B1中点，点Q在侧面DCC1D1内运动，若∠PBQ=∠PBD，则动点Q的轨迹所在曲线为（ ）| A． | 圆 | B． | 椭圆 | C． | 双曲线 | D． | 抛物线 |
分析 先确定∠PBQ是定值，利用平面DCC1D1∥BP，可得动点Q的轨迹所在曲线为双曲线．
解答 解：∵∠PBQ=∠PBD，∴∠PBQ是定值，
∵平面DCC1D1∥BP，
∴动点Q的轨迹所在曲线为双曲线，
故选：C．
点评 本题考查立体几何中的轨迹问题，考查考查圆锥曲线的定义，比较基础．
练习册系列答案
相关题目
10．已知定义域为R的奇函数f（x）的周期为4，且x∈（0，2）时f（x）=ln（x2-x+b），若函数f（x）在区间[-2，2]上恰有5个零点，则实数b应满足的条件是（ ）
| A． | -1＜b≤1 | B． | -1＜b＜1或b=$\frac{5}{4}$ | C． | $\frac{1}{4}$＜b$≤\frac{5}{4}$ | D． | $\frac{1}{4}$＜b≤1或b=$\frac{5}{4}$ |
17．已知函数f（x）的图象如图：则满足f（2x）•f（lg（x2-6x+120））≤0的x的取值范围是（ ）
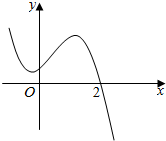
| A． | （-∞，1] | B． | [1，+∞） | C． | [0，+∞） | D． | （-∞，2] |
14．下列函数中，在定义域内单调递增，且在区间（-1，1）内有零点的函数是（ ）
| A． | y=log${\;}_{\frac{1}{2}}$x | B． | y=2x-1 | C． | $y={x^2}-\frac{1}{2}$ | D． | y=-x3 |