题目内容
设函数f(x)=(1+x)2-ln(1+x)2.(1)求函数f(x)的单调区间;
(2)当x∈[![]() -1,e-1]时,不等式f(x)<m恒成立,求实数m的取值范围;
-1,e-1]时,不等式f(x)<m恒成立,求实数m的取值范围;
(3)关于x的方程f(x)=x2+x+a在[0,2]上恰有两个相异实根,求实数a的取值范围.(e为自然常数,约等于2.718 281 828 459)
解:(1)函数定义域为(-∞,-1)∪(-1,+∞),∵f′(x)=2[(x+1)![]() ]=
]=![]() ,
,
由f′(x)>0,得-2<x<-1或x>0;由f′(x)<0,得x<-2或-1<x<0,
则递增区间是(-2,-1),(0,+∞),递减区间是(-∞,-2),(-1,0).
(2)由f′(x)=![]() =0,得x=0或x=-2.
=0,得x=0或x=-2.
由(1)知,f(x)在[![]() -1,0]上递减,在[0,e-1]上递增.
-1,0]上递减,在[0,e-1]上递增.
又f(![]() -1)=
-1)=![]() +2,f(e-1)=e2-2,且e2-2>
+2,f(e-1)=e2-2,且e2-2>![]() +2,∴x∈[
+2,∴x∈[![]() -1,e-1]时,[f(x)]max=e2-2,
-1,e-1]时,[f(x)]max=e2-2,
故m>e2-2时,不等式f(x)<m恒成立.
(3)方程f(x)=x2+x+a,即x-a+1-ln(1+x)2=0.记g(x)=x-a+1-ln(1+x)2,
则g′(x)=1![]() =
=![]() .由g′(x)>0,得x<-1或x>1,由g′(x)<0,得-1<x<1.
.由g′(x)>0,得x<-1或x>1,由g′(x)<0,得-1<x<1.
∴g(x)在[0,1]上递减,在[1,2]上递增.
为使f(x)=x2+x+a在[0,2]上恰好有两个相异的实根,只需g(x)=0在[0,1)和(1,2]上各有一个实根,于是有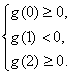 解得2-2ln2<a≤3-2ln3.
解得2-2ln2<a≤3-2ln3.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设函数f(x)=
,则
(a≠b)的值是( )
|
| (a+b)-(a-b)f(a-b) |
| 2 |
| A、a | B、b |
| C、a,b中较小的数 | D、a,b中较大的数 |
设函数f(x)=
的反函数为h(x),又函数g(x)与h(x+1)的图象关于有线y=x对称,则g(2)的值为( )
| 1-x |
| 1+x |
A、-
| ||
B、-
| ||
| C、-1 | ||
| D、-2 |
设函数f(x)=
,若方程f(x)=a有且只有一个实根,则实数a满足( )
|
| A、a<0 | B、0≤a<1 |
| C、a=1 | D、a>1 |