Question

【题目】已知椭圆，直线不过原点且不平行于坐标轴，与有两个交点，，线段的中点为.证明：

（）直线的斜率与的斜率的乘积为定值.

（）若过点，延长线段与交于点，当四边形为平行四边形时，则直线的斜率.

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

（1）利用点差法即可证明；

（2）根据题意M是平行四边形对角线的交点，利用坐标关系代换，构造齐次式解，再根据（1）的结论证得结论.

（1）设，直线不经过原点且不与坐标轴平行，

所以 ，

直线的斜率，直线的斜率，

，在椭圆上，两式相减：

，两边同时除以

得，所以，

即

所以直线的斜率与的斜率的乘积为定值；

（2）四边形为平行四边形时，当且仅当与互相平分，

设，则，且在椭圆上，，即

由（1）得，，

所以，

整理得：，又因为

所以，即，两边平方得：

， ，

所以两边同时除以，

，

所以，

，

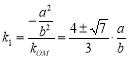所以