题目内容
已知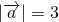 ,
,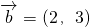
(1)若 ,求
,求 ; (2)若
; (2)若 ,求
,求 .
.
解:(1)设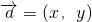 ,∵
,∵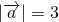 ,∴x2+y2=9…①
,∴x2+y2=9…①
又∵ ∴
∴ 即2x+y=0…②…(3分)
即2x+y=0…②…(3分)
由①②可解得: 或
或
∴ …(6分)
…(6分)
(2)设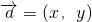 (3),∵
(3),∵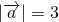 ,∴x2+y2=9(4)…(5)①
,∴x2+y2=9(4)…(5)①
又∵ ∴x=2y…②…(9分)
∴x=2y…②…(9分)
由①②可解得: 或
或
∴ …(12分)
…(12分)
分析:(1)设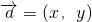 ,由于
,由于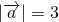 利用向量模的公式得x2+y2=9,由
利用向量模的公式得x2+y2=9,由 ⊥
⊥ ,
, •
• =0,我们易构造一个关于x,y的方程,解方程即可求出满足条件的x,y的值,从而得出答案.
=0,我们易构造一个关于x,y的方程,解方程即可求出满足条件的x,y的值,从而得出答案.
(2)若 ∥
∥ ,根据两个向量平行,坐标交叉相乘差为零,构造一个关于x,y的方程,解方程求出x,y的值后,即可得到
,根据两个向量平行,坐标交叉相乘差为零,构造一个关于x,y的方程,解方程求出x,y的值后,即可得到 .
.
点评:本题考查的知识是数量积判断两个平面向量的垂直关系,向量的模,平行向量与共线向量,其中根据“两个向量平行,坐标交叉相乘差为零,两个向量若垂直,对应相乘和为零”构造方程是解答本题的关键.
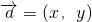 ,∵
,∵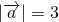 ,∴x2+y2=9…①
,∴x2+y2=9…①又∵
 ∴
∴ 即2x+y=0…②…(3分)
即2x+y=0…②…(3分)由①②可解得:
 或
或
∴
 …(6分)
…(6分)(2)设
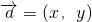 (3),∵
(3),∵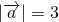 ,∴x2+y2=9(4)…(5)①
,∴x2+y2=9(4)…(5)①又∵
 ∴x=2y…②…(9分)
∴x=2y…②…(9分)由①②可解得:
 或
或
∴
 …(12分)
…(12分)分析:(1)设
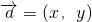 ,由于
,由于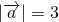 利用向量模的公式得x2+y2=9,由
利用向量模的公式得x2+y2=9,由 ⊥
⊥ ,
, •
• =0,我们易构造一个关于x,y的方程,解方程即可求出满足条件的x,y的值,从而得出答案.
=0,我们易构造一个关于x,y的方程,解方程即可求出满足条件的x,y的值,从而得出答案.(2)若
 ∥
∥ ,根据两个向量平行,坐标交叉相乘差为零,构造一个关于x,y的方程,解方程求出x,y的值后,即可得到
,根据两个向量平行,坐标交叉相乘差为零,构造一个关于x,y的方程,解方程求出x,y的值后,即可得到 .
.点评:本题考查的知识是数量积判断两个平面向量的垂直关系,向量的模,平行向量与共线向量,其中根据“两个向量平行,坐标交叉相乘差为零,两个向量若垂直,对应相乘和为零”构造方程是解答本题的关键.

练习册系列答案
相关题目

 ,求
,求 实数的值;
实数的值; ,求实数
,求实数
 ,求函数
,求函数 在点(0,
在点(0, )处的切线方程;
)处的切线方程; ,使得
,使得 的极大值为3.若存在,求出
的极大值为3.若存在,求出 ,
, ,求
,求 的值;
的值; ,求
,求 中含
中含 项的系数
项的系数
 ,求m的值;
,求m的值; ,求m的取值范围。
,求m的取值范围。