题目内容

已知数列{an}中，a1=5且an=3an-1+3n-1(n≥2).

(1)求a2,a3的值;

(2)设bn=，是否存在实数λ，使数列{bn}为等差数列，若存在请求其通项bn,若不存在,请说明理由.

解析：(1)a2=23,a3=95.

(2)设存在实数λ满足题意由b1+b3=2b2,得,即9（5+λ）+95+λ=6(23+λ).

∴λ=.当n≥2时

bn-bn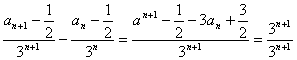-1==1.

∴{bn}是等差数列.

∵首项b1=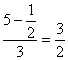,公差d=1,

∴bn=+(n-1)×1，即bn=n+.

练习册系列答案
相关题目
已知数列{an}中，a1=1，an+1-an=
1
3n+1
(n∈N*)，则
lim
n→∞
an=
 
．
已知数列{an}中，a1=1，an+1=
an
1+2an
，则{an}的通项公式an=
1
2n-1
1
2n-1
．
已知数列{an}中，a1=1，a1+2a2+3a3+…+nan=
n+1
2
an+1(n∈N*)．
（1）求数列{an}的通项公式；
（2）求数列{
2n
an
}的前n项和Tn．
已知数列{an}中，a1=
1
2
，Sn为数列的前n项和，且Sn与
1
an
的一个等比中项为n(n∈N*），则
lim
n→∞
Sn=
1
1
．
已知数列{an}中，a1=1，2nan+1=（n+1）an，则数列{an}的通项公式为（　　）
A、
n
2n
B、
n
2n-1
C、
n
2n-1
D、
n+1
2n

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网