题目内容
已知函数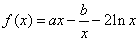 ,
,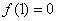
( I ) 若函数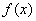 在其定义域内为单调函数,求
在其定义域内为单调函数,求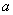 的取值范围;
的取值范围;
( II ) 若函数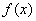 的图像在x=1处的切线斜率为0,且
的图像在x=1处的切线斜率为0,且
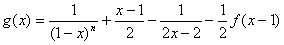 ,(
,(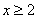 ,
,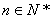 )
)
证明:对任意的正整数n,当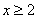 时,有
时,有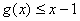 .
.
(1)函数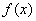 的定义域是
的定义域是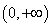
因为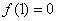 所以有
所以有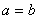 所以
所以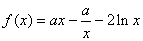 (1分)
(1分)
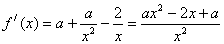 (2分)
(2分)
当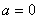 时,
时,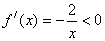 恒成立,所以函数
恒成立,所以函数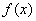 在
在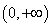 上单调递减; (3分)
上单调递减; (3分)
当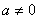 时,
时,
若函数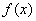 在其定义域内单调递增,则有
在其定义域内单调递增,则有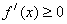 恒成立即
恒成立即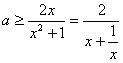
因为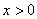 所以
所以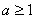 且
且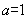 时
时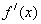 不恒为0. (4分)
不恒为0. (4分)
若函数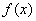 在其定义域内单调递减,则有
在其定义域内单调递减,则有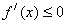 恒成立即
恒成立即
因为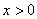 所以
所以
综上,函数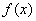 在定义域内单调时
在定义域内单调时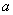 的取值范围是
的取值范围是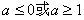 (5分)
(5分)
(2)因为函数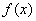 的图像在x=1处的切线斜率为0,所以
的图像在x=1处的切线斜率为0,所以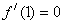
即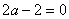 所以
所以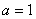
所以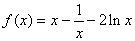 (6分)
(6分)
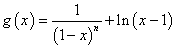
令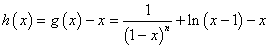 说明 此处可有多种构造函数的方法,通
说明 此处可有多种构造函数的方法,通
所以 (7分) 常均需要讨论n是奇数还是偶数
(7分) 常均需要讨论n是奇数还是偶数
当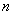 是偶数时,因为
是偶数时,因为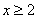 所以
所以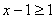 可参照答案所示 每种情况酌情赋2-3分
可参照答案所示 每种情况酌情赋2-3分
所以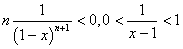
所以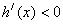 即函数
即函数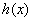 在
在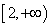 单调递减
单调递减
所以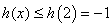 ,即
,即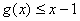 (9分)
(9分)
当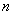 是奇数时,令
是奇数时,令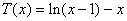 则
则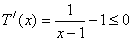
所以函数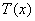 在
在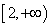 单调递减,所以
单调递减,所以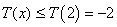 (10分)
(10分)
又因为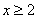 时
时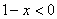 所以
所以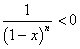
所以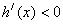 即函数
即函数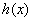 在
在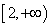 单调递减 (11分)
单调递减 (11分)
所以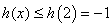 ,即
,即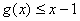
综上,对任意的正整数n,当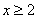 时,有
时,有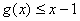 .(12分)
.(12分)

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 的前n项和
的前n项和
 ,求数列
,求数列 的前
的前 项和
项和
 ,若
,若 ,则
,则 _______
_______ ,若对于任意的正数
,若对于任意的正数 都是其定义域上的增函数,则函数
都是其定义域上的增函数,则函数 B.
B. 
 D.
D. 
 的内角
的内角 所对的边是
所对的边是 ,且
,且
 ;
;  的值.
的值.  为等差数列,且
为等差数列,且 ,则
,则 的值为
的值为  B.
B.  C.
C.  D.
D. 
 的方程
的方程
 (其中
(其中 是自然对数的底数)的有三个不
是自然对数的底数)的有三个不 的取值范围是
的取值范围是 } D. {
} D. { }
} 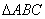 中,
中, 为边
为边 上任意一点,
上任意一点, 为
为 的中点,
的中点, ,则
,则 的值为( )
的值为( )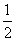 B、
B、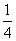 C、
C、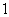 D、
D、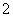
 ,那么它的体积为
,那么它的体积为 B.
B. C.
C.  D.
D. 