题目内容

设数列{a_n}是等差数列，a₁＜0，a₇•a₈＜0．若数列{a_n}的前n项的和S_n取得最小值，则n的值为

A.
4
B.
7
C.
8
D.
15

B
分析：由已知得到首项和公差之间的关系，再结合a₁＜0分析出数列递增，求出哪几项为负值即可得到结论．
解答：∵a₁＜0，a₇•a₈＜0．
∴d＞0，a₇＜0，a₈＞0
∴数列{a_n}的前n项的和S_n取得最小值时，n=7
故选B
点评：本题主要考查等差数列的前n项和以及数列的函数特性．解决本题的关键是由a₁＜0分析出数列递增．

练习册系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

小升初全能卷系列答案

小升初全优模拟大考卷系列答案

考试先锋小升初全真模拟试卷系列答案

小升初衔接教材系列答案

学业水平总复习系列答案

毕业升学总动员系列答案

日练周测新语思英语系列答案

全优中考系统总复习系列答案

相关题目

设数列{a_n}是等差数列，数列{b_n}是各项都为正数的等比数列，且a₁=b₁=1，b₁+b₂=a₂，b₃是a₁与a₄的等差中项．
（I）求数列{a_n}，{b_n}的通项公式；
（II）求数列{

}的前n项和S_n．

（2012•枣庄一模）设数列{a_n}满足a₁=1，a₂=2，对任意的n∈N^*，a_n+2是a_n+1与a_n的等差中项．
（1）设b_n=a_n+1-a_n，证明数列{b_n}是等比数列，并求出其通项公式；
（2）写出数列{a_n}的通项公式（不要求计算过程），令cn=

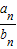-an)，求数列{c_n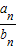}的前n项和S_n．

设数列{a_n}是等差数列，数列{b_n}是各项都为正数的等比数列，且a₁=b₁=1，b₁+b₂=a₂，b₃是a₁与a₄的等差中项．
（I）求数列{a_n}，{b_n}的通项公式；
（II）求数列{

}的前n项和S_n．

设数列{a_n}是等差数列，数列{b_n}是各项都为正数的等比数列，且a₁=b₁=1，b₁+b₂=a₂，b₃是a₁与a₄的等差中项．
（I）求数列{a_n}，{b_n}的通项公式；
（II）求数列{

}的前n项和S_n．

设数列{a_n}是等差数列，数列{b_n}是各项都为正数的等比数列，且a₁=b₁=1，b₁+b₂=a₂，b₃是a₁与a₄的等差中项．
（I）求数列{a_n}，{b_n}的通项公式；
（II）求数列{

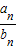}的前n项和S_n．