题目内容
13.设a≥0,b≥0,$\frac{{b}^{2}}{2}$+a2=1,则a$\sqrt{1-{b}^{2}}$的最大值为1.分析 由题意可得b2+2a2=2,代入可得a$\sqrt{1-{b}^{2}}$=$\sqrt{2({a}^{2}-\frac{1}{4})^{2}-\frac{1}{8}}$,又可得$\frac{1}{2}$≤a2≤1,由二次函数区间的值域可得.
解答 解:∵a≥0,b≥0,$\frac{{b}^{2}}{2}$+a2=1,
∴b2+2a2=2,∴1-b2=2a2-1,
∴a$\sqrt{1-{b}^{2}}$=a$\sqrt{2{a}^{2}-1}$=$\sqrt{{a}^{2}(2{a}^{2}-1)}$
=$\sqrt{2{a}^{4}-{a}^{2}}$=$\sqrt{2({a}^{2}-\frac{1}{4})^{2}-\frac{1}{8}}$,
∵b2=2-2a2≥0,1-b2=2a2-1≥0,
∴$\frac{1}{2}$≤a2≤1,由二次函数可知,
当a2=1时,a$\sqrt{1-{b}^{2}}$取最大值1,
故答案为:1.
点评 本题考查函数的值域,涉及二次函数的值域,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 中,点
中,点 ,直线
,直线 ,设圆
,设圆 的半径为
的半径为 ,圆心在
,圆心在 上.
上.
 上,过点
上,过点 作圆
作圆 ,使
,使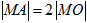 ,求圆心
,求圆心 的取值范围.
的取值范围. ,则
,则 ( )
( ) B.
B. C.
C. D.
D.

 如图,给出16个点,其左和右相邻两点,上下相邻两点的距离都为1,若以这些点为三角形的顶点,那么一共可得到200个直角三角形.
如图,给出16个点,其左和右相邻两点,上下相邻两点的距离都为1,若以这些点为三角形的顶点,那么一共可得到200个直角三角形.