题目内容
18.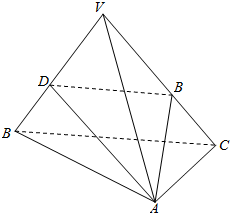 设正三棱锥V-ABC的底面边长为4,侧棱长为8,过A作与侧棱VB,VC相交的截面AED,求截面三角形AED的周长的最小值.
设正三棱锥V-ABC的底面边长为4,侧棱长为8,过A作与侧棱VB,VC相交的截面AED,求截面三角形AED的周长的最小值.
分析 根据给出的正三棱锥的侧棱长和底面边长知,两条侧棱的夹角为锐角,然后求出该锐角的三倍角的余弦值,使原图形中的△AEF的周长最小,就是求沿PA剪开再展开后A点与A′点的最短距离,即直线距离,运用余弦定理可求解.
解答 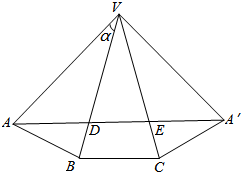 解:沿三棱锥V-ABC的侧棱VA剪开后再展开,如图,
解:沿三棱锥V-ABC的侧棱VA剪开后再展开,如图,
原图中△AED的周长最小,也就是展开图中的AA′,
在△VAB中,因为VA=VB=8,AB=4,
设∠APB=α,则cosα=$\frac{{VA}^{2}+{VB}^{2}-{AB}^{2}}{2VA•VB•}$=$\frac{{8}^{2}+{8}^{2}-{4}^{2}}{2×8×8}$=$\frac{7}{8}$.
∠AVA′=3α,
由cos3α=4cos3α-3cosα=4×($\frac{7}{8}$)3-3×$\frac{7}{8}$=$\frac{7}{128}$.
在△APA′中,由余弦定理得:
AA′2=VA2+VA′2-2VA•VA′cos3α
=82+82-2×8×8×$\frac{7}{128}$
=121.
所以,AA′=11.
所以,△AED的周长最小值为11.
点评 本题考查了棱锥的结构特征,考查了距离最短问题,该类问题通常比喻“蚂蚁爬行问题”,解答的方法是沿一定的棱或母线把多面体或旋转体剪开,然后再展开,求两点间的直线距离问题,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知抛物线x2=2py(p>0)的焦点与双曲线x2-y2=-$\frac{1}{2}$的一个焦点重合,且在抛物线上有一动点P到x轴的距离为m,P到直线l:2x-y-4=0的距离为n,则m+n的最小值为( )
| A. | $\sqrt{5}$+1 | B. | $\sqrt{5}$-1 | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$-2 |
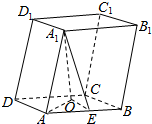 如图,斜四边形ABCD-A1B1C1D1的底面是边长为8cm的正方形,侧棱AA1成为12cm,且上底面的顶点A1与下底面各点间的距离相等,则四棱柱的侧面积是$32\sqrt{15}$.
如图,斜四边形ABCD-A1B1C1D1的底面是边长为8cm的正方形,侧棱AA1成为12cm,且上底面的顶点A1与下底面各点间的距离相等,则四棱柱的侧面积是$32\sqrt{15}$.
 如图,△ABC为等腰直角三角形,∠ACB=90°,PA⊥面ABC,AC=a,PA=$\sqrt{2}$a.
如图,△ABC为等腰直角三角形,∠ACB=90°,PA⊥面ABC,AC=a,PA=$\sqrt{2}$a.