Question

设正项数列{a_n}的前n项和为S_n，且a₁=2，a_n+1=2S_n+2（n∈N^*），
（1）求a₂以及数列{a_n}的通项公式；
（2）在a_n与a_n+1之间插入n个数，使这n个数组成一个公差为d_n的等差数列．
（ⅰ）求证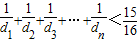：（n∈N^*）；
（ⅱ）求证：在数列{d_n}中不存在三项d_m，d_s，d_t成等比数列．（其中m，s，t依次成等比数列）

Answer 1

【答案】分析：（1）由a₁=2，a_n+1=2S_n+2（n∈N^*），知a₂=2S₁+2=6，由a_n+1=2S_n+2，得a_n+2=2S_n+1+2，由此能求出．
（2）（ⅰ）由题意可知，，通过错项相减能够证明（n∈N^*）．
（ⅱ）假设数列{d_n}中存在三项d_m，d_s，d_t成等比数列，则，推导出m=s=t，由题设知m=s=t不成立，故在数列{d_n}中不存在三项d_m，d_s，d_t成等比数列．
解答：解：（1）∵a₁=2，a_n+1=2S_n+2（n∈N^*），
∴a₂=2S₁+2=2×2+2=6，
由a_n+1=2S_n+2，
得a_n+2=2S_n+1+2，
两式相减得a_n+2=3a_n+1，
又a₂=3a₁，且a_n≠0，
所以数列{a_n}是等比数列，
且a₁=2，q=3，
∴．
（2）（ⅰ）由题意可知
，
，
通过错项相减求得；
（ⅱ）假设数列{d_n}中存在三项d_m，d_s，d_t成等比数列，
则，
即，
整理，得（=，
∴，
∴m，s，t依次成等比数列，且m，s，t依次成等差数列，
∴m=s=t，
∵，在a_n与a_n+1之间插入n个数，使这n个数组成一个公差为d_n的等差数列，
∴m=s=t不成立，
∴在数列{d_n}中不存在三项d_m，d_s，d_t成等比数列．
点评：本题考查数列的通项公式的证明，考查不等式的证明和数列不可能是等比数列的证明．解题时要认真审题，仔细解答，注意错位相减法和反证法的合理运用．