题目内容
12.在平面直角坐标系xOy中,A(-1,0),B(0,2),C(2,0).(1)求过点C且与AB垂直的直线l的方程;
(2)求以点C为圆心且与AB相切的圆的方程.
分析 (1)利用相互垂直的直线斜率之间的关系、点斜式即可得出.
(2)利用圆与直线AB相切的条件是:圆心到直线的距离=圆的半径,求出圆的半径,可得圆的标准方程.
解答 解:(1)∵kAB=$\frac{2-0}{0-(-1)}$=2,∴kl=-$\frac{1}{2}$,----------(3分)
∴l的方程为y-0=-$\frac{1}{2}$(x-2),即x+2y-2=0.-------------------------(6分)
(2)AB所在的直线方程为y=2(x+1),即2x-y+2=0,-------------------(8分)
点C到直线AB的距离d=$\frac{6}{\sqrt{5}}$=$\frac{6}{5}\sqrt{5}$,-----------------------------(10分)
∴以点C为圆心且与AB相切的圆的方程为(x-2)2+y2=$\frac{36}{5}$.-------------(12分)
点评 本题考查了斜率计算公式、相互垂直的直线斜率之间的关系、点斜式,考查了直线与圆的位置关系及圆的标准方程,属于基础题.

练习册系列答案
相关题目
2.在如图所示的四个图示中,是结构图的是( )
| A. | 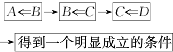 | B. | 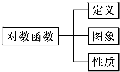 | ||
| C. | 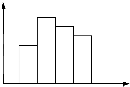 | D. | 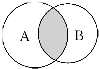 |
3.b,c表示两条不重合的直线,α,β表示两个不重合的平面,下列命题中正确的是( )
| A. | $\left.\begin{array}{l}{c∥α}\\{b?α}\end{array}\right\}$⇒c∥b | B. | $\left.\begin{array}{l}{c∥α}\\{α⊥β}\end{array}\right\}$⇒c⊥β | C. | $\left.\begin{array}{l}{c⊥α}\\{c⊥β}\end{array}\right\}$⇒α∥β | D. | $\left.\begin{array}{l}{b∥c}\\{c?α}\end{array}\right\}$⇒b∥α |
7.定义:$\frac{n}{{p}_{1}+{p}_{1}+…+{p}_{n}}$为n个p1,p2,…pn的“均倒数”,若已知正数数列{an}的前n项的”均倒数“为$\frac{1}{2n+1}$,又bn=$\frac{{a}_{n}-1}{2}$.,$\frac{1}{{b}_{1}{b}_{2}}$+$\frac{1}{{b}_{2}{b}_{3}}$+…+$\frac{1}{{b}_{2014}{b}_{2015}}$=( )
| A. | $\frac{2013}{4027}$ | B. | $\frac{4026}{4027}$ | C. | $\frac{2014}{4029}$ | D. | $\frac{4028}{4029}$ |
17.若实数a,b满足a2+b2≤1,则关于x的方程x2-ax+$\frac{3}{4}$b2=0有实数根的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | 1 |
4.已知函数f(x)满足f(x+4)=f(x),且当-1<x≤3时,f(x)=$\left\{\begin{array}{l}{m\sqrt{1-{x}^{2}},x∈(-1,1]}\\{1-|x-2|,x∈(1,3]}\end{array}\right.$.其中m>0,若方程3f(x)-x=0恰好有5个根,则实数m的取值范围是( )
| A. | ($\frac{\sqrt{15}}{3}$,$\sqrt{7}$) | B. | ($\frac{\sqrt{15}}{3}$,$\frac{8}{3}$) | C. | ($\frac{4}{3}$,$\sqrt{7}$) | D. | ( $\frac{4}{3}$,$\frac{8}{3}$) |
1.设复数z1=-1+i,z2=$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i,则$\frac{{z}_{1}}{{z}_{2}}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.某几何体的三视图如图所示,它的表面积为( )
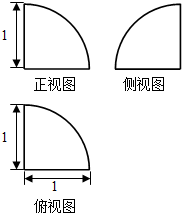

| A. | $\frac{π}{4}$ | B. | $\frac{5π}{4}$ | C. | $\frac{7π}{8}$ | D. | π |