题目内容
17．若实数a，b满足a2+b2≤1，则关于x的方程x2-ax+$\frac{3}{4}$b2=0有实数根的概率是（ ）| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | 1 |
分析 求出方程有解的等价条件，利用几何概型的概率公式即可得到结论
解答 解：实数a，b满足a2+b2≤1，对应的区域是以1为半径的圆，
关于x的方程x2-ax+$\frac{3}{4}$b2=0有实数根，则判别式△=a2-4×$\frac{3}{4}$b2=a2-3b2≥0，
即（a-$\sqrt{3}$）（a+$\sqrt{3}$）≥0，
作出不等式组对应的平面区域如图：
则a-$\sqrt{3}$b=0的斜率k=$\frac{\sqrt{3}}{3}$，对应的倾斜角为30°，
a+$\sqrt{3}$b=0的斜率k=-$\frac{\sqrt{3}}{3}$，对应的倾斜角为150°，
∴两条直线的夹角为60°，
∴根据几何概型的概率公式可得所求的概率P=$\frac{2×60°}{360°}=\frac{1}{3}$；
故选：C
点评 本题主要考查几何概型的概率的计算，根据条件求出对应区域是解决本题的关键
练习册系列答案
相关题目
5．某超市从2014年甲、乙两种酸奶的日销售量（单位：箱）的数据中分別随机抽取100个．整理得到数据分组及频率分布表和频率分布直方图：
（Ⅰ）写出频率分布直方图1中的a的值；并作出甲种酸奶日销售量的频率分布直方图；
（Ⅱ）记甲种酸奶与乙种酸奶日销售量（单位：箱）的方差分别为s${\;}_{1}^{2}$，s${\;}_{2}^{2}$，试比较s${\;}_{1}^{2}$与s${\;}_{2}^{2}$的大小；（只需写出结论）
（Ⅲ）假设同一组中的每个数据可用该该组区间的中点值代替，试估计乙种酸奶在未来一个月（按30天计箅）的销售量总量．
| 分组（日销售量） | 频率（甲种酸奶） |
| [0，10] | 0.10 |
| （10，20] | 0.20 |
| （20，30] | 0.30 |
| （30，40] | 0.25 |
| （40，50] | 0.15 |
（Ⅰ）写出频率分布直方图1中的a的值；并作出甲种酸奶日销售量的频率分布直方图；
（Ⅱ）记甲种酸奶与乙种酸奶日销售量（单位：箱）的方差分别为s${\;}_{1}^{2}$，s${\;}_{2}^{2}$，试比较s${\;}_{1}^{2}$与s${\;}_{2}^{2}$的大小；（只需写出结论）
（Ⅲ）假设同一组中的每个数据可用该该组区间的中点值代替，试估计乙种酸奶在未来一个月（按30天计箅）的销售量总量．
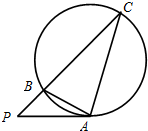如图，过圆外一点P作圆的切线PA（A为切点），再作割线PBC依次交圆于B，C．若PA=6，PB=3，AB=4，则AC=8．