Question

【题目】如图，ABCD是正方形，O是正方形的中心，PO底面ABCD，E是PC的中点。

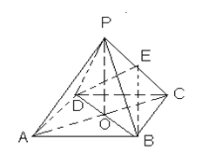
求证：（1）PA∥平面BDE ；

（2）平面PAC平面BDE.

Answer 1

【答案】证明：（Ⅰ）连结EO，

在△PAC中，∵O是AC的中点，E是PC的中点，

∴OE∥AP

又∵OE平面BDE，

PA平面BDE，

∴PA∥平面BDE

（Ⅱ）∵PO底面ABCD，

∴POBD

又∵ACBD，且ACPO＝O，

∴BD平面PAC．

而BD平面BDE，

∴平面PAC平面BDE。

【解析】

证明：（Ⅰ）连结EO，

在△PAC中，∵O是AC的中点，E是PC的中点，

∴OE∥AP．

又∵OE平面BDE，

PA平面BDE，

∴PA∥平面BDE．

（Ⅱ）∵PO底面ABCD，

∴POBD．

又∵ACBD，且ACPO＝O，

∴BD平面PAC．

而BD平面BDE，

∴平面PAC平面BDE．