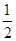题目内容
在长为 的线段
的线段 上任取一点
上任取一点 现作一矩形,领边长分别等于线段
现作一矩形,领边长分别等于线段 的长,则该矩形面积小于
的长,则该矩形面积小于 的概率为( )
的概率为( )
A. | B.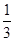 | C.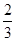 | D. |
C
解析试题分析:设AC=x,则0<x<12,若矩形面积为小于32,则x>8或x<4,从而利用几何概型概率计算公式,所求概率为长度之比解:设AC=x,则BC=12-x,0<x<12
若矩形面积S=x(12-x)<32,则x>8或x<4,即将线段AB三等分,当C位于首段和尾段时,矩形面积小于32,故该矩形面积小于32cm2的概率为P== 故选 C
故选 C
考点:几何概型
点评:本题主要考查了几何概型概率的意义及其计算方法,将此概率转化为长度之比是解决本题的关键,属基础题

练习册系列答案
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
在某一试验中事件A出现的概率为 ,则在
,则在 次试验中
次试验中 出现
出现 次的概率为( )
次的概率为( )
A.1- | B. |
C.1- | D. |
两位大学毕业生一起去一家单位应聘,面试前单位负责人对他们说:“我们要从面试的人中招聘3人,你们俩同时被招聘进来的概率是 ”,根据这位负责人的话可以推断出参加面试的人数为( ).
”,根据这位负责人的话可以推断出参加面试的人数为( ).
| A.20 | B.21 | C.10 | D.70 |
设 为两个事件,且
为两个事件,且 ,
, ,则( )
,则( )
A. 与 与 互斥 互斥 | B. 与 与 对立 对立 | C. | D.A、B、C都不对 |




 B.
B. C.
C.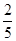 D.
D.




 则满足
则满足 的学生成绩情况的概率是
的学生成绩情况的概率是



 ,以点
,以点 ,求弦
,求弦