题目内容
已知空间向量
=(sinα,-1,cosα),
=(1,2cosα,1),
•
=
,α∈(0,
)
(1)求sin2α及sinα,cosα的值;
(2)设函数f(x)=5cos(2x-a)+cos2x(x∈R),求f(x)的最小正周期及f(x)取得最大值时x的值.
| a |
| b |
| a |
| b |
| 1 |
| 5 |
| π |
| 2 |
(1)求sin2α及sinα,cosα的值;
(2)设函数f(x)=5cos(2x-a)+cos2x(x∈R),求f(x)的最小正周期及f(x)取得最大值时x的值.
分析:(1)利用向量的数量积公式结合同角三角函数公式,即可求sin2α及sinα,cosα的值;
(2)先化简函数,在利用正弦函数的性质,即可得到结论.
(2)先化简函数,在利用正弦函数的性质,即可得到结论.
解答:解:(1)∵
=(sinα,-1,cosα),
=(1,2cosα,1),
•
=
,
∴sinα-cosα=
①,
∴1-2sinαcosα=
,∴sin2α=
②
联立①,②解得:sinα=
,cosα=
(2)f(x)=5cos(2x-α)+cos2x=5cos2xcosα+5sin2xsinα+cos2x
=3cos2x+4sin2x+cos2x=4(sin2x+cos2x)=4
sin(2x+
)
∴f(x)的最小正周期T=π
当2x+
=2kπ+
时,f(x)max=4
,此时x=kπ+
,(k∈Z).
| a |
| b |
| a |
| b |
| 1 |
| 5 |
∴sinα-cosα=
| 1 |
| 5 |
∴1-2sinαcosα=
| 1 |
| 25 |
| 24 |
| 25 |
联立①,②解得:sinα=
| 4 |
| 5 |
| 3 |
| 5 |
(2)f(x)=5cos(2x-α)+cos2x=5cos2xcosα+5sin2xsinα+cos2x
=3cos2x+4sin2x+cos2x=4(sin2x+cos2x)=4
| 2 |
| π |
| 4 |
∴f(x)的最小正周期T=π
当2x+
| π |
| 4 |
| π |
| 2 |
| 2 |
| π |
| 8 |
点评:本题考查向量的数量积公式、同角三角函数公式,考查三角函数的化简,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S; 分别与向量
分别与向量 ,求向量
,求向量 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S; 分别与向量
分别与向量 ,求向量
,求向量 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S;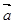 分别与向量
分别与向量 ,求向量
,求向量 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S; 分别与向量
分别与向量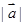 =
= ,求向量
,求向量