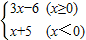题目内容
已知f(x)=10|lgx|,若方程f(x)=b(b是实常数)有两个不同的实数根x1、x2,则2x1+x2的最小值是________.
2
分析:由方程f(x)=b,即方程10|lgx|=b,即|lgx|=lgb,根据题意知lgx1=lgb,lgx2=lgb,从而得出两个不同的实数根之积为定值,再根据基本不等式即可得出2x1+x2的最小值.
解答:方程f(x)=b,即方程10|lgx|=b,
从而|lgx|=lgb,
若方程f(x)=b(b是实常数)有两个不同的实数根x1、x2,
则lgx1=lgb,lgx2=lgb,
∴lgx1+lgx2=0,x1x2=1.
∴2x1+x2≥2 =2
=2 ,当且仅当2x1=x2取等号,
,当且仅当2x1=x2取等号,
则2x1+x2的最小值是 2 .
.
故答案为:2 .
.
点评:本题主要考查了基本不等式、函数的零点与方程根的关系等基本知识,属于基础题.

分析:由方程f(x)=b,即方程10|lgx|=b,即|lgx|=lgb,根据题意知lgx1=lgb,lgx2=lgb,从而得出两个不同的实数根之积为定值,再根据基本不等式即可得出2x1+x2的最小值.
解答:方程f(x)=b,即方程10|lgx|=b,
从而|lgx|=lgb,
若方程f(x)=b(b是实常数)有两个不同的实数根x1、x2,
则lgx1=lgb,lgx2=lgb,
∴lgx1+lgx2=0,x1x2=1.
∴2x1+x2≥2
 =2
=2 ,当且仅当2x1=x2取等号,
,当且仅当2x1=x2取等号,则2x1+x2的最小值是 2
 .
.故答案为:2
 .
.点评:本题主要考查了基本不等式、函数的零点与方程根的关系等基本知识,属于基础题.

练习册系列答案
相关题目