题目内容
设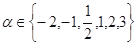 ,则使幂函数
,则使幂函数 为奇函数且在
为奇函数且在 上单调递增的a值的个数为( )
上单调递增的a值的个数为( )
| A.0 | B.1 | C.2 | D.3 |
C
解析试题分析:因为 是奇函数,所以
是奇函数,所以 应该为奇数,又在
应该为奇数,又在 是单调递增的,所以
是单调递增的,所以 则只能1,3.
则只能1,3.
考点:幂函数的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若

 ,
, ,则
,则 的大小关系为( )
的大小关系为( )
A. | B. | C. | D. |
若函数 在点
在点 处连续,则
处连续,则 的值为( )
的值为( )
| A.10 | B.20 | C.15 | D.25 |
设 ,
, ,
, ,则
,则 之间的大小关系是( )
之间的大小关系是( )
A. | B. | C. | D. |
已知 ,
, ,
, ,
, ,则下列等式一定成立的是( )
,则下列等式一定成立的是( )
A. | B. | C. | D. |
已知函数 是R上的奇函数,且当
是R上的奇函数,且当 时,
时, ,设函数
,设函数  ,若
,若

 ,则实数
,则实数 的取值范围是( )
的取值范围是( )
A. | B. |
| C.(1,2) | D. |
 ,其中
,其中 .
.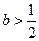 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性; ,不等式
,不等式 都成立.
都成立. 时,在同一坐标系中,函数
时,在同一坐标系中,函数 与
与 的图像是( )
的图像是( )
 ,第二年的增长率为
,第二年的增长率为 ,则该市这两年生产总值的年平均增长率为( )
,则该市这两年生产总值的年平均增长率为( )


