题目内容
已知t>-1,当x∈[-t,t+2]时,函数y=(x-4)|x|的最小值为-4,则t的取值范围是 .
分析:画出函数y=(x-4)|x|=
的图象,结合区间[-t,t+2]关于直线x=1对称及已知,构造关于t的不等式组,解不等式组,可得t的取值范围.
|
解答: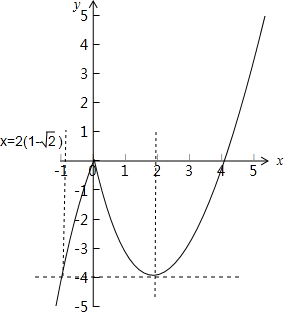 解:函数y=(x-4)|x|=
解:函数y=(x-4)|x|=
的图象如下图所示:
由区间[-t,t+2]关于直线x=1对称,且函数y=(x-4)|x|的最小值为-4,
故
解得t∈[0,2
-2]
故t的取值范围是[0,2
-2]
故答案为:[0,2
-2]
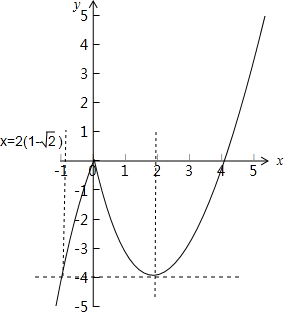 解:函数y=(x-4)|x|=
解:函数y=(x-4)|x|=
|
由区间[-t,t+2]关于直线x=1对称,且函数y=(x-4)|x|的最小值为-4,
故
|
解得t∈[0,2
| 2 |
故t的取值范围是[0,2
| 2 |
故答案为:[0,2
| 2 |
点评:本题考查的知识点是函数的最值及其几何意义,其中根据函数的图象及已知条件,构造关于t的不等式组,是解答的关键.

练习册系列答案
相关题目