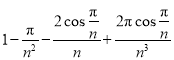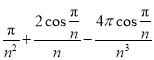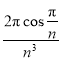Question

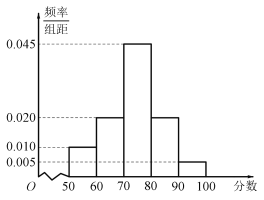
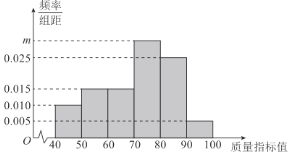
【题目】在全球抗击新冠肺炎疫情期间，我国医疗物资生产企业加班加点生产口罩、防护服、消毒水等防疫物品，保障抗疫一线医疗物资供应，在国际社会上贏得一片赞誉．我国某口罩生产厂商在加大生产的同时．狠抓质量管理，不定时抽查口罩质量，该厂质检人员从某日所生产的口罩中随机抽取了100个，将其质量指标值分成以下五组：，，，，，得到如下频率分布直方图．

（1）规定：口罩的质量指标值越高，说明该口罩质量越好，其中质量指标值低于130的为二级口罩，质量指标值不低于130的为一级口罩．现从样本口罩中利用分层抽样的方法随机抽取8个口罩，再从中抽取3个，记其中一级口罩个数为，求的分布列及数学期望；

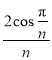（2）在2020年“五一”劳动节前，甲，乙两人计划同时在该型号口罩的某网络购物平台上分别参加、两店各一个订单“秒杀”抢购，其中每个订单由个该型号口罩构成．假定甲、乙两人在、两店订单“秒杀”成功的概率分别为，，记甲、乙两人抢购成功的订单总数量、口罩总数量分别为，，

①求的分布列及数学期望；

②求当的数学期望取最大值时正整数的值．

Answer 1

【答案】（1）见解析，（2）①见解析；②6

【解析】

（1）根据分层抽样可得二级、一级口罩个数，然后写出的所有可得取值并计算相应的概率，列出分布列并根据数学期望公式可得结果.

（2）①写出写出的所有可得取值并计算相应的概率，列出分布列并根据数学期望公式可得结果.②根据，使用换元法并构造函数，然后利用导数判断函数单调性，进一步可得取最大值的条件.

（1）按分层抽样抽取8个口罩，则其中二级、一级口罩个数分别为6，2．故的可能取值为0，1，2．

，

，

，

的分布列为

	0	1	2

所以．

（2）①由题知的可能取值为0，1，2，

；

；

．

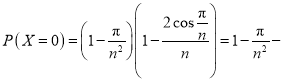
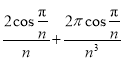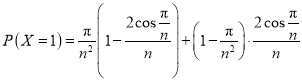
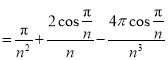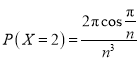所以的分布列为

	0	1	2

所以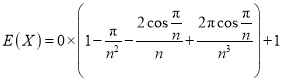

．

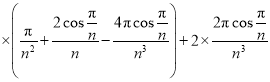
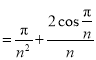②因为，

所以，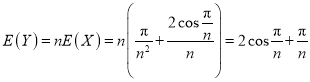

令，

设，

则，

因为，

所以当时，，

所以在区间上单调递增；

当时，，

所以在区间上单调递减；

所以当即时取最大值，

所以．

所以取最大值时，的值为6．