Question

【题目】命题方程表示双曲线；命题不等式的解集是. 为假， 为真，求的取值范围.

【答案】

【解析】试题分析：由命题方程表示双曲线，求出的取值范围，由命题不等式的解集是，求出的取值范围，由为假， 为真，得出一真一假，分两种情况即可得出的取值范围.

试题解析：

真

，

真 或

∴

真假

假真

∴范围为

【题型】解答题
【结束】
18

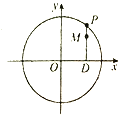
【题目】如图，设是圆上的动点，点是在轴上的投影， 为上一点，且.

（1）当在圆上运动时，求点的轨迹的方程；

（2）求过点且斜率为的直线被所截线段的长度.

Answer 1

【答案】（1）.（2）.

【解析】试题分析：（1）由题意可知：M的坐标为（x，y），P的坐标为（x'，y'），则，得，代入，整理得： .

（2）设直线方程为： ，代入椭圆方程，由韦达定理可知：x1+x2=3，x1x2=-8，弦长公式：丨AB丨=即可求得直线被C所截线段的长度．

试题解析：

（1）设点的坐标为，点的坐标为，由已知得.

∵在圆上， ，

即，整理得，即的方程为.

（2）过点且斜率为的直线方程为，

设直线与的交点为， ，将直线方程代入的方程，

得，即.

∴x1+x2=3，x1x2=-8∴线段的长度为

.

∴直线被所截线段的长度为.