题目内容
已知数列{bn}中,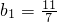 ,bn+1bn=bn+2.数列{an}满足:
,bn+1bn=bn+2.数列{an}满足: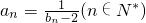
(Ⅰ)求证:an+1+2an+1=0;
(Ⅱ) 求数列{an}的通项公式;
(Ⅲ) 求证:(-1)b1+(-1)2b2+…+(-1)nbn<1(n∈N*)
证明:(Ⅰ) ,移向整理得an+1+2an+1=0
,移向整理得an+1+2an+1=0
解:(Ⅱ)∵an+1=-2an-1∴
又 ∴
∴ 为等比数列
为等比数列
∴ ∴
∴
证明:(Ⅲ) ∴
∴
①当n为奇数时(-1)nbn+(-1)n+1bn+1= =
=
(-1)b1+(-1)2b2+…+(-1)nbn
 =
=
②当n为偶数时,(-1)b1+(-1)2b2+…+(-1)nbn

综上所述,(-1)b1+(-1)2b2+…+(-1)nbn<1
分析:(Ⅰ) 由已知,得出 ,移向整理即可.
,移向整理即可.
(Ⅱ)在(Ⅰ) 的基础上,构造出 ,通过求出
,通过求出 的通项公式,得出{an}的通项公式.
的通项公式,得出{an}的通项公式.
(Ⅲ)由上应得出 ,考虑到(-1)n的取值,宜相邻两项结合,借助放缩法寻求解决.
,考虑到(-1)n的取值,宜相邻两项结合,借助放缩法寻求解决.
点评:本题是数列与不等式的综合.考查数列的递推关系,通项公式、不等式的证明.考查变形、构造、转化、计算的能力.
 ,移向整理得an+1+2an+1=0
,移向整理得an+1+2an+1=0解:(Ⅱ)∵an+1=-2an-1∴

又
 ∴
∴ 为等比数列
为等比数列∴
 ∴
∴
证明:(Ⅲ)
 ∴
∴
①当n为奇数时(-1)nbn+(-1)n+1bn+1=
 =
=
(-1)b1+(-1)2b2+…+(-1)nbn

 =
=
②当n为偶数时,(-1)b1+(-1)2b2+…+(-1)nbn


综上所述,(-1)b1+(-1)2b2+…+(-1)nbn<1
分析:(Ⅰ) 由已知,得出
 ,移向整理即可.
,移向整理即可.(Ⅱ)在(Ⅰ) 的基础上,构造出
 ,通过求出
,通过求出 的通项公式,得出{an}的通项公式.
的通项公式,得出{an}的通项公式.(Ⅲ)由上应得出
 ,考虑到(-1)n的取值,宜相邻两项结合,借助放缩法寻求解决.
,考虑到(-1)n的取值,宜相邻两项结合,借助放缩法寻求解决.点评:本题是数列与不等式的综合.考查数列的递推关系,通项公式、不等式的证明.考查变形、构造、转化、计算的能力.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 ,
, ,数列{an}满足:
,数列{an}满足: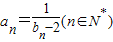 .
.