题目内容
【题目】在平面直角坐标系中,O为原点,两个点列![]() 和
和![]() 满足:①
满足:①![]() ;②
;②![]()
(1)求点![]() 和
和![]() 的坐标;
的坐标;
(2)求向量![]() 的坐标;
的坐标;
(3)对于正整数k,用![]() 表示无穷数列
表示无穷数列![]() 中从第k+1项开始的各项之和,用
中从第k+1项开始的各项之和,用![]() 表示无穷数列
表示无穷数列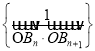 中从第k项开始的各项之和,即
中从第k项开始的各项之和,即![]() ,
,![]() 若存在正整数k和p,使得
若存在正整数k和p,使得![]() ,求k,p的值.
,求k,p的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)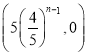 ,
,![]() ;(3)见解析
;(3)见解析
【解析】
(1)求出![]() ,从而
,从而![]() ,
,![]() ,由此能求出点A3和B3的坐标.
,由此能求出点A3和B3的坐标.
(2)由AnAn+1=(![]() )n﹣1A1A2=(﹣(
)n﹣1A1A2=(﹣(![]() )n﹣1,0),得到
)n﹣1,0),得到![]() ,由此能求出向量
,由此能求出向量![]() ,
,![]() 的坐标.
的坐标.
(3)由|![]() |=5(
|=5(![]() )n﹣1,得
)n﹣1,得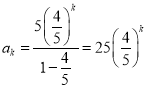 ,
,![]() ,从而25(
,从而25(![]() )k=2kp,由此能求出结果.
)k=2kp,由此能求出结果.
(1)![]() ,故
,故![]() ,即
,即![]() ;
;![]() ,故
,故![]() ,即
,即![]()
(2)由已知,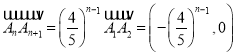 ,
,
故![]() =
=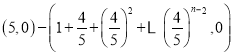 =
=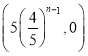
而![]() ;
;
(3)![]() ,
,![]() ,
,
故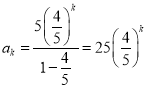 ,
,![]() ,
,
由已知,![]() ,所以,左边为正整数,故k=1或2;
,所以,左边为正整数,故k=1或2;
当k=1时,2p=20,得p=10;
当k=2时,4p=16,得p=4.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目