题目内容
(本小题满分12分)
已知定义域为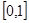 的函数
的函数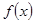 同时满足以下三个条件:
同时满足以下三个条件:
①对任意的 ,总有
,总有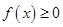 ;
;
②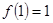 ;
;
③若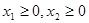 且
且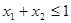 ,则有
,则有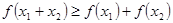 成立,则称
成立,则称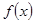 为“友谊函数”。
为“友谊函数”。
(1)若已知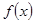 为“友谊函数”,求
为“友谊函数”,求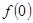 的值;
的值;
(2)函数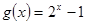 在区间
在区间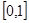 上是否为“友谊函数”?并给出理由;
上是否为“友谊函数”?并给出理由;
(3)已知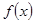 为“友谊函数”,且
为“友谊函数”,且 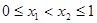 ,求证:
,求证: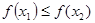 。
。
已知定义域为
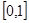 的函数
的函数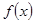 同时满足以下三个条件:
同时满足以下三个条件:①对任意的
 ,总有
,总有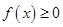 ;
;②
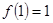 ;
;③若
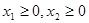 且
且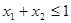 ,则有
,则有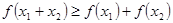 成立,则称
成立,则称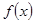 为“友谊函数”。
为“友谊函数”。(1)若已知
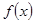 为“友谊函数”,求
为“友谊函数”,求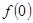 的值;
的值;(2)函数
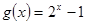 在区间
在区间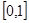 上是否为“友谊函数”?并给出理由;
上是否为“友谊函数”?并给出理由;(3)已知
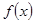 为“友谊函数”,且
为“友谊函数”,且 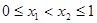 ,求证:
,求证: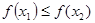 。
。(1)取 得
得 ,又由
,又由 ,得
,得
(2)显然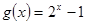 在
在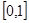 上满足①
上满足① ②
② ;
;
③若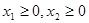 ,且
,且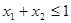 ,
,
则有
故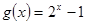 满足条件①﹑②﹑③所以
满足条件①﹑②﹑③所以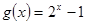 为友谊函数。……8分
为友谊函数。……8分
(3)因为 ,则0<
,则0< <1,
<1,
所以 .
.
 得
得 ,又由
,又由 ,得
,得
(2)显然
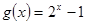 在
在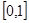 上满足①
上满足① ②
② ;
;③若
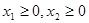 ,且
,且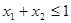 ,
,则有

故
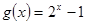 满足条件①﹑②﹑③所以
满足条件①﹑②﹑③所以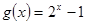 为友谊函数。……8分
为友谊函数。……8分(3)因为
 ,则0<
,则0< <1,
<1,所以
 .
.略

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
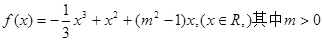
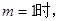 曲线
曲线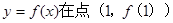 处的切线方程
处的切线方程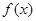 有三个互不相同的零点0,
有三个互不相同的零点0,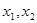 ,且
,且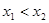 。若对任意的
。若对任意的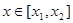 ,
,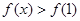 恒成立,求m的取值范围。
恒成立,求m的取值范围。 ,问其中是否有模型能完全符合公司的要求?说明理由.
,问其中是否有模型能完全符合公司的要求?说明理由. )
) 格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为l0.假设不计其它成本,即销售每套丛书的利润 = 售价 一 供货价格.问:
格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为l0.假设不计其它成本,即销售每套丛书的利润 = 售价 一 供货价格.问: 书定价为100元时,书商能获得的总利润是多少万元?
书定价为100元时,书商能获得的总利润是多少万元? 的定义域是一切实数
的定义域是一切实数 ,且
,且 ,求
,求 的值”。请问
的值”。请问 (元)与月处理量
(元)与月处理量 (吨)之间的函数关系式可近似的表示为:
(吨)之间的函数关系式可近似的表示为: ,且每处理一吨二氧化碳得到可利用的化工产品价值为300元。
,且每处理一吨二氧化碳得到可利用的化工产品价值为300元。 的解集为
的解集为 ,那么函数
,那么函数 的图象大致是( )
的图象大致是( )
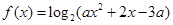 ,
,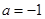 时,求该函数的定义域和值域;
时,求该函数的定义域和值域;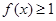 在区间
在区间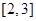 上恒成立,求实数
上恒成立,求实数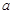 的取值范围.
的取值范围.