题目内容
设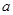 ,
,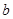 ,
,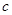 是空间三条直线,
是空间三条直线,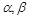 是空间两个平面,则下列命题中,逆命题不成立
是空间两个平面,则下列命题中,逆命题不成立
的是 ( )
A.当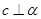 时,若 时,若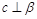 ,则 ,则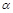 ∥ ∥ |
B.当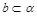 时,若 时,若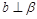 ,则 ,则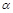 ⊥ ⊥ |
C.当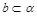 ,且c是a在 ,且c是a在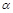 内的射影时,若 内的射影时,若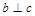 ,则 ,则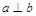 |
D.当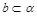 ,且 ,且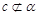 时, 时,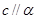 ,则 ,则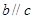 |
B
解析试题分析:A、其逆命题是:当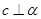 时,或
时,或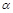 ∥
∥ ,则
,则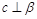 ,由面面平行的性质定理知正确.
,由面面平行的性质定理知正确.
B、其逆命题是:当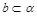 ,若
,若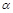 ⊥
⊥ ,则
,则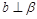 ,也可能平行,相交.不正确.
,也可能平行,相交.不正确.
C、其逆命题是当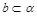 ,且
,且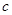 是
是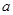 在
在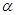 内的射影时,若
内的射影时,若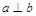 ,则
,则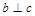 ,由三垂线定理知正确.
,由三垂线定理知正确.
D、其逆命题是当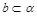 ,且
,且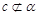 时,若
时,若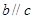 ,则
,则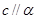 ,由线面平行的判定定理知正确.故选B
,由线面平行的判定定理知正确.故选B
考点:平面与平面之间的位置关系;四种命题;空间中直线与直线之间的位置关系.
点评:本题主要考查线面平行的判定理,三垂线定理及其逆定理,面面平行的性质定理等,做这样的题目要多观察几何体效果会更好.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
“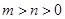 ”是“方程
”是“方程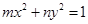 表示焦点在y轴上的椭圆”的
表示焦点在y轴上的椭圆”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列命题中正确的是( )
A.函数 与 与 互为反函数 互为反函数 |
B.函数 与 与 都是增函数 都是增函数 |
C.函数 与 与 都是奇函数 都是奇函数 |
D.函数 与 与 都是周期函数 都是周期函数 |
“x>1”是“ >x”的( )
>x”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
由命题“存在x∈R,使e|x-1|-m≤0”是假命题,得m的取值范围是(-∞,a),则实数a的取值是( )
| A.(-∞,1) | B.(-∞,2) | C.1 | D.2 |
下列有关命题的说法正确的是( )
A.命题“若 ,则 ,则 ”的否命题为“若 ”的否命题为“若 ,则 ,则 ” ” |
B.命题“ ”的否定是“ ”的否定是“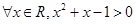 ” ” |
C.命题“若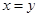 ,则 ,则 ”的逆否命题为假命题 ”的逆否命题为假命题 |
| D.若“p或q”为真命题,则p,q至少有一个为真命题 |
命题“若A∩B=A,则A B的逆否命题是( )
B的逆否命题是( )
A.若A∪B≠A,则A B B | B.若A∩B≠A,则A B B |
C.若A B,则A∩B≠A B,则A∩B≠A | D.若A B,则A∩B≠A B,则A∩B≠A |
给出命题:已知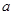 、
、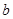 为实数,若
为实数,若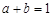 ,则
,则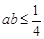 .在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是( )
.在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是( )
| A.3 | B.2 | C.1 | D.0 |