题目内容
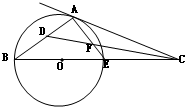 已知C点在圆O直径BE的延长线上,CA切圆O于A点,∠ACB的平分线分别交AE、AB于点F、D.
已知C点在圆O直径BE的延长线上,CA切圆O于A点,∠ACB的平分线分别交AE、AB于点F、D.(1)求∠ADF的度数;
(2)若AB=AC,求
| AC | BC |
分析:(1)由已知中C点在圆O直径BE的延长线上,CA切圆O于A点,∠ACB的平分线分别交AE、AB于点F、D根据弦切角定理,三角形外角定理,及圆周角定理的推论,我可判断出△ADF为等腰直角三角形,进而可得∠ADF的度数;
(2)若AB=AC,结合(1)的结论,我们可得△ABC三个角分别为30°,30°,120°,解三角形,即可得到
的值.
(2)若AB=AC,结合(1)的结论,我们可得△ABC三个角分别为30°,30°,120°,解三角形,即可得到
| AC |
| BC |
解答:解:(1)∵CA切圆O于A点,
由弦切角定理,
可得∠CAE=∠B
又∵CD为∠ACB的角平分线,
∴∠ACD=∠BCD
∴∠ACD+∠CAE=∠B+∠BCD
即∠ADF=∠AFD
又∵BE为圆O的直径
∴∠DAF=90°
∴∠ADF=45°
(2)若AB=AC,则∠CAE=∠B=∠ACB=30°
则
=
由弦切角定理,
可得∠CAE=∠B
又∵CD为∠ACB的角平分线,
∴∠ACD=∠BCD
∴∠ACD+∠CAE=∠B+∠BCD
即∠ADF=∠AFD
又∵BE为圆O的直径
∴∠DAF=90°
∴∠ADF=45°
(2)若AB=AC,则∠CAE=∠B=∠ACB=30°
则
| AC |
| BC |
| ||
| 3 |
点评:本题考查的知识点是圆周角定理,弦切角定理,三角形外角定理,本题没有给出任何角而求角,故思路一定是证明未知角是特殊角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
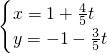 (t为参数)被曲线
(t为参数)被曲线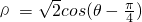 所截的弦长为________.
所截的弦长为________.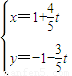 (t为参数)被曲线
(t为参数)被曲线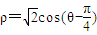 所截的弦长为 .
所截的弦长为 . (t为参数)被曲线
(t为参数)被曲线 所截的弦长为 .
所截的弦长为 .