题目内容
直线y=x+b与曲线y=
有且仅有一个公共点,则b的取值范围是
| x2-1 |
b≥1或-1≤b<0
b≥1或-1≤b<0
.分析:先整理曲线y=
的方程可知曲线y=
的图象为双曲线的一部分,要满足仅有一个公共点,有两种情况,一种是与左部分相交,另一种是与右部分相交,根据图象可分别求得b的上限和下限,最后综合可求得b的范围.
| x2-1 |
| x2-1 |
解答: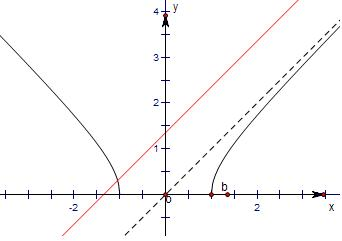 解:依题意可知曲线y=
解:依题意可知曲线y=
的方程可整理成x2-y2=1(y≥0)
要使直线y=x+b与曲线y=
仅有一个公共点,有两种情况,如图.
(1)直线与左部分相交,
即b≥1;
(2)直线与右部分相交,
此时b的范围为-1≤b<0.
综合得b的范围:b≥1或-1≤b<0.
故答案为:b≥1或-1≤b<0.
 解:依题意可知曲线y=
解:依题意可知曲线y=| x2-1 |
要使直线y=x+b与曲线y=
| x2-1 |
(1)直线与左部分相交,
即b≥1;
(2)直线与右部分相交,
此时b的范围为-1≤b<0.
综合得b的范围:b≥1或-1≤b<0.
故答案为:b≥1或-1≤b<0.
点评:本题主要考查了直线与双曲线的位置关系.考查了学生对数形结合思想,转化和化归的思想的综合运用.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
若直线y=x-b与曲线
(θ∈[0,2π))有两个不同的公共点,则实数b的取值范围为( ).
|
A、(2-
| ||||
B、[2-
| ||||
C、(-∞,2-
| ||||
D、(2-
|
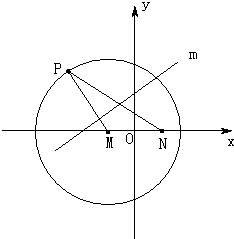 如图,已知
如图,已知